In system the magnitude of the force is 100 dynes. In another system where the fundamental phyical quamtities are kilogram , meter , and minute, find the magnitude of the force.
To find the magnitude of the force in a system where the fundamental physical quantities are kilogram, meter, and minute, we will convert the force from the CGS system (dynes) to this new system. Here are the steps:
Step 1: Understand the conversion of units
1 Dyne is defined as the force required to accelerate a mass of 1 gram at a rate of 1 cm/s². Therefore, we can express 1 Dyne in terms of kilograms, meters, and minutes.
Step 2: Convert the units
- Convert grams to kilograms:
1 gram=10−3 kg
- Convert centimeters to meters:
1 cm=10−2 m
- Convert seconds to minutes:
1 second=160 minutes
Step 3: Substitute the conversions into the Dyne definition
Using the conversions, we can express 1 Dyne as:
1 Dyne=1 gram⋅1 cm/s2=(10−3 kg)⋅(10−2 m)⋅(160 min)−2
Step 4: Calculate the conversion factor
Substituting the values:
1 Dyne=10−3 kg⋅10−2 m⋅(36001 min2)
Calculating this gives:
1 Dyne=10−3⋅10−2⋅3600 kg m/min2
=3.6×10−5 kg m/min2
Step 5: Calculate the force in the new system
Now, we need to convert 100 dynes to the new system:
100 Dynes=100×(3.6×10−5 kg m/min2)
Calculating this gives:
=3.6×10−3 kg m/min2
Final Result
Thus, the magnitude of the force in the new system is:
Magnitude of the force=3.6×10−3 kg m/min2
---
1 Dyne is defined as the force required to accelerate a mass of 1 gram at a rate of 1 cm/s². Therefore, we can express 1 Dyne in terms of kilograms, meters, and minutes.
- Convert grams to kilograms:
1 gram=10−3 kg
- Convert centimeters to meters:
1 cm=10−2 m
1 second=160 minutes
Using the conversions, we can express 1 Dyne as:
1 Dyne=1 gram⋅1 cm/s2=(10−3 kg)⋅(10−2 m)⋅(160 min)−2
Substituting the values:
1 Dyne=10−3 kg⋅10−2 m⋅(36001 min2)
Calculating this gives:
1 Dyne=10−3⋅10−2⋅3600 kg m/min2
=3.6×10−5 kg m/min2
Now, we need to convert 100 dynes to the new system:
100 Dynes=100×(3.6×10−5 kg m/min2)
Calculating this gives:
=3.6×10−3 kg m/min2
Thus, the magnitude of the force in the new system is:
Magnitude of the force=3.6×10−3 kg m/min2
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.1
16 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.2
6 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
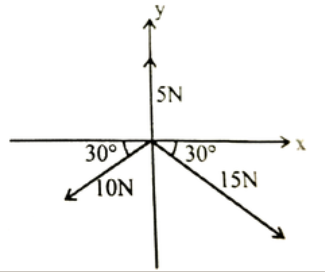
Find the magnitude of the resultant of shown forces :-
View Solutionfind the magnitude of dipole moment of the the following system

View SolutionFind the magnitudes of the unknown forces if the sum of all forces is zero (figure)

View SolutionFind the magnitude of the unknown forces X and Y if sum of all forces is zero.

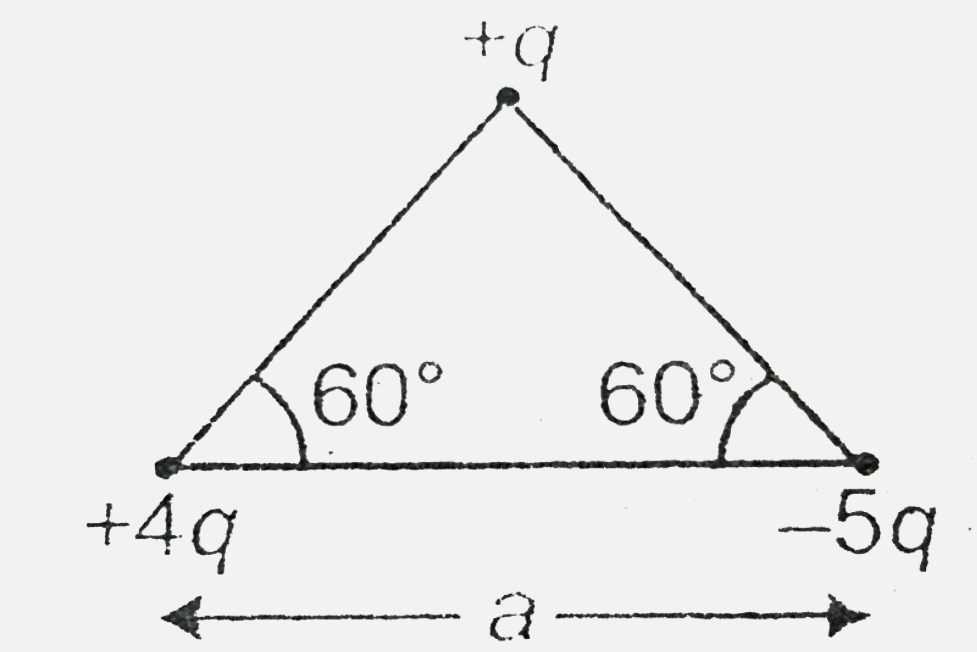
View SolutionFind the magnitude of dipole moment of the following system.
View SolutionSum of magnitude of two forces is 20 N and magnitude of their resultant is 10 N. If resultant is perpendicular to the smaller force find values of both forces.
View SolutionTwo forces whose magnitudes are in the ratio 3:5 give a resultant of 28N. If the angle of their inclination is 60∘, find the magnitude of each force.
View SolutionTwo forces whose magnitudes are in the ratio 3:5 give a resultant of 28N. If the angle of their inclination is 60∘, find the magnitude of each force.
View SolutionFour forces of magnitude P, 2P, 3P and 4P act along the four sides of a square ABCD in cyclic order. Use the vector method to find the magnitude of resultant force.
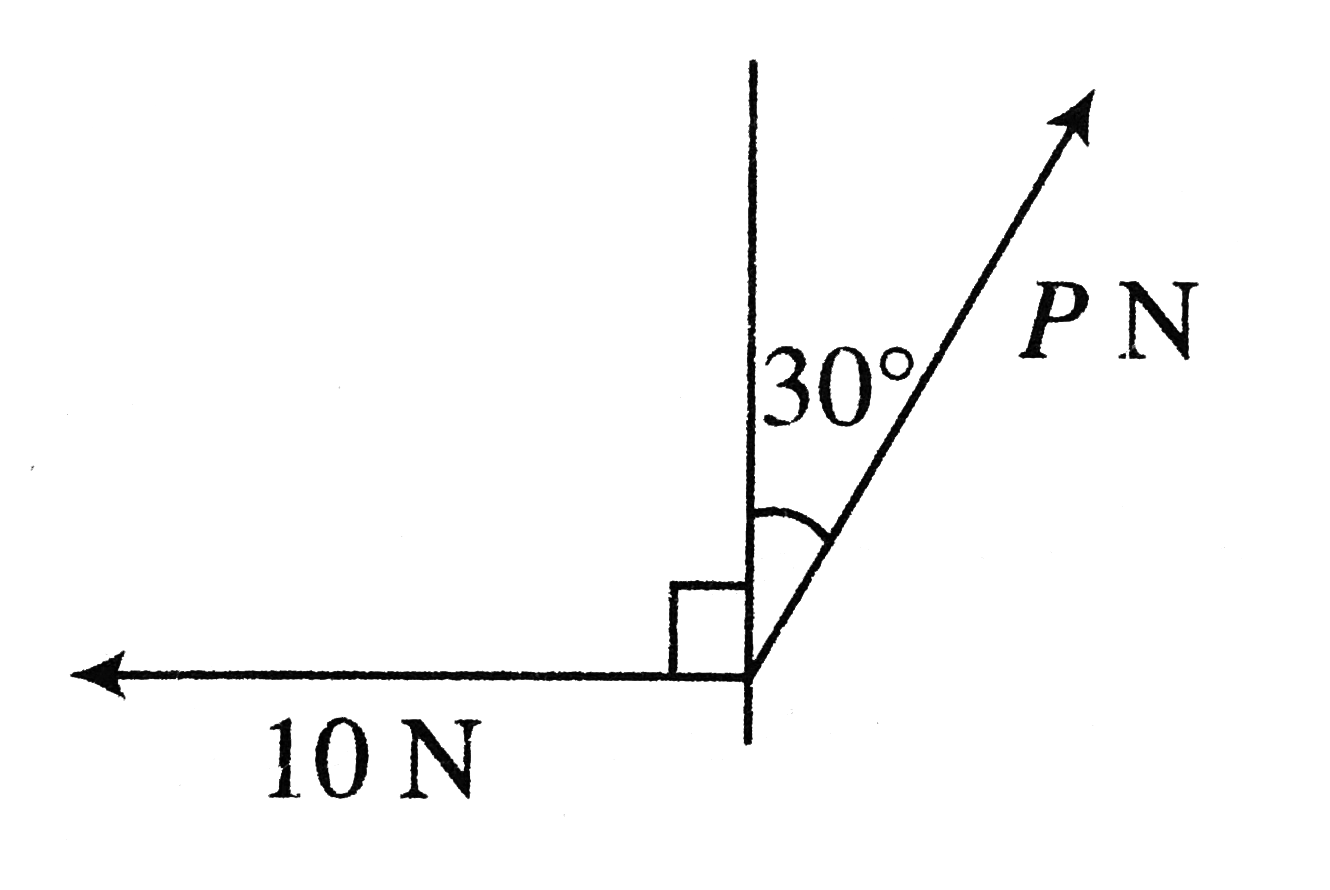
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
View Solution
