At a certain instant, a stationary transverse wave is found to have maximum kinetic energy. The appearance of string at that instant is
sinusoidal shape with amplitude A/3
sinusoidal with amplitude A/2
sinusoidal shape with amplitude A
straight line
The correct Answer is:D
To solve the problem, we need to analyze the behavior of a stationary transverse wave and its kinetic energy at a specific instant. Here's a step-by-step breakdown:
Step 1: Understand the nature of stationary transverse waves
A stationary transverse wave is formed by the superposition of two waves traveling in opposite directions. In such a wave, certain points (nodes) remain stationary, while others (antinodes) oscillate with maximum amplitude.
Hint: Recall that in a stationary wave, particles oscillate about their mean position.
Step 2: Identify the condition for maximum kinetic energy
In simple harmonic motion (SHM), the kinetic energy of a particle is maximum when it is at its mean position (the equilibrium position). This is because, at this point, the particle has the highest velocity.
Hint: Remember that kinetic energy is related to the velocity of the particles in SHM.
Step 3: Relate the kinetic energy condition to the wave
For the entire string to have maximum kinetic energy at a certain instant, all particles of the string must be at their mean positions simultaneously. This means that the wave must not have any displacement from the mean position at that instant.
Hint: Think about what the shape of the wave would look like if all points are at their mean position.
Step 4: Determine the appearance of the string
If all particles of the string are at their mean positions, the wave will appear as a straight line. This is because there will be no oscillation or displacement from the equilibrium position at that instant.
Hint: Visualize the wave: if every point is at the mean position, how would the wave look?
Step 5: Conclusion
Given that all particles are at their mean position, the appearance of the string at that instant will be a straight line.
Final Answer: The appearance of the string at that instant is a straight line.
A stationary transverse wave is formed by the superposition of two waves traveling in opposite directions. In such a wave, certain points (nodes) remain stationary, while others (antinodes) oscillate with maximum amplitude.
In simple harmonic motion (SHM), the kinetic energy of a particle is maximum when it is at its mean position (the equilibrium position). This is because, at this point, the particle has the highest velocity.
For the entire string to have maximum kinetic energy at a certain instant, all particles of the string must be at their mean positions simultaneously. This means that the wave must not have any displacement from the mean position at that instant.
If all particles of the string are at their mean positions, the wave will appear as a straight line. This is because there will be no oscillation or displacement from the equilibrium position at that instant.
Given that all particles are at their mean position, the appearance of the string at that instant will be a straight line.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:NDA EXAM QUESTIONS
Explore 55 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OSCILLATIONS
Explore 23 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
In case of a transverses wave in a string
View SolutionIn an L-C oscillation maximum charge on capacitor can be Q0 . If at any instant electrical energy is th 34 of the magnetic energy then the charge on capacitor at that instant is
View SolutionA transverse wave is travelling on a string. The equation of the wave
View SolutionA particle is released from a height S. At certain height its kinetic energy is three times its potential energy. The height and speed of the particle at that instant are respectively
View SolutionA solid sphere is rolling on a rough surface, whose centre of mass is at C at a certain instant. Find at that instant it has angular velocity ω. Its radius is R. Find the angular acceleration at that instant mass of sphere is m

View SolutionStatement I : Maximum changes of pressure and density occur at the nodal points of the medium in a stationary transverse wave produced in the medium
Statement II : There will be compressions and rarefractions in a stationary longitudinal wave at the nodal points.
View SolutionWhich of the following will have maximum total kinetic energy at temperature 300 K
View SolutionIn a stationary wave along a string the strain is
View SolutionA particle starts simple harmonic motion from the mean position. Its amplitude is a and total energy E . At one instant its kinetic energy is 3E/4 . Its displacement at that instant is
View SolutionThe figure here gives the electric field of an EM wave at a certain point and a certain. The wave is transporting energy in the negative z direction. What is the direction of the magnetic field of the wave at the point and instant?
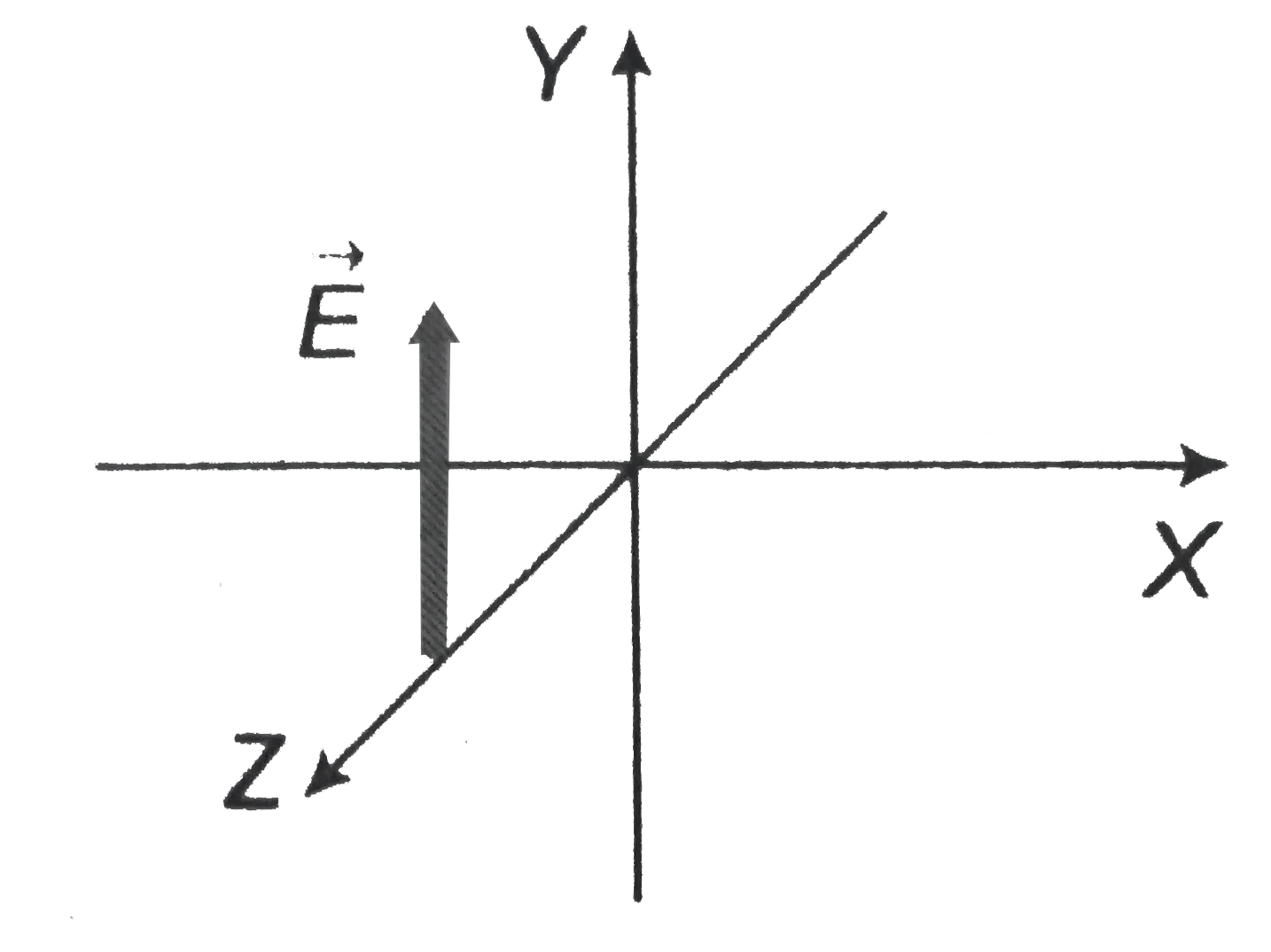
A. Towards + X direction
B. Towards - X direction
C. Towards + direction
D. Towards - Z direction
View Solution

