In an adiabatic change the pressure and temperature of monoatomic gas are related as P∝Tc where C equal
2/5
5/2
3/5
5/3
The correct Answer is:B
To solve the problem, we need to establish the relationship between pressure (P) and temperature (T) for a monoatomic gas undergoing an adiabatic process. The steps are as follows:
Step 1: Understand the Adiabatic Process
In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) can be described using the equation:
PVγ=constant
where γ (gamma) is the heat capacity ratio Cp/Cv.
Step 2: Express Volume in Terms of Pressure and Temperature
Using the ideal gas law:
PV=nRT
we can express volume (V) as:
V=nRTP
Step 3: Substitute Volume into the Adiabatic Equation
Substituting the expression for V into the adiabatic equation:
P(nRTP)γ=constant
This simplifies to:
P1−γ(nRT)γ=constant
Step 4: Rearranging the Equation
Rearranging gives us:
P1−γ∝(nRT)γ
This implies:
P1−γ∝Tγ
Step 5: Expressing Pressure in Terms of Temperature
From the proportional relationship, we can express pressure as:
P∝Tγ1−γ
Step 6: Identifying the Value of C
Comparing this with the given relationship P∝TC, we find that:
C=γ1−γ
Step 7: Finding the Value of Gamma for Monoatomic Gas
For a monoatomic gas, the value of γ is:
γ=CpCv=53
Step 8: Substituting Gamma into the Expression for C
Substituting γ into the expression for C:
C=531−53=53−23=−52
Step 9: Finalizing the Value of C
Thus, we find:
C=52
Conclusion
The value of C for the relationship between pressure and temperature in an adiabatic process for a monoatomic gas is:
C=52
In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) can be described using the equation:
PVγ=constant
where γ (gamma) is the heat capacity ratio Cp/Cv.
Using the ideal gas law:
PV=nRT
we can express volume (V) as:
V=nRTP
Substituting the expression for V into the adiabatic equation:
P(nRTP)γ=constant
This simplifies to:
P1−γ(nRT)γ=constant
Rearranging gives us:
P1−γ∝(nRT)γ
This implies:
P1−γ∝Tγ
From the proportional relationship, we can express pressure as:
P∝Tγ1−γ
Comparing this with the given relationship P∝TC, we find that:
C=γ1−γ
For a monoatomic gas, the value of γ is:
γ=CpCv=53
Substituting γ into the expression for C:
C=531−53=53−23=−52
Thus, we find:
C=52
The value of C for the relationship between pressure and temperature in an adiabatic process for a monoatomic gas is:
C=52
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:THERMAL CONDUCTION
Explore 17 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:THERMAL RADIATION
Explore 13 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (CALORIMETRY, CHANGE OF STATE & KINETIC THEORY OF GASES )
Explore 30 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
In an adiabatic change, the pressure p and temperature T of a diatomic gas are related by the relation p∝Tα, where α equals
View SolutionAn ideal gas undergoing adiabatic change has the following pressure-temperature relationship
View SolutionFor a monoatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume TVx = constant, where x is
View SolutionSome ideal monoatomic gas A in an enclosure has a pressure P and the temperature T . Another ideal monoatomic gas B enclosed in a container of the same volume has a pressure of 2P and temperature T2. The ratio of the average kinetic energy per molecule of gas A to gas B is
View SolutionA monoatomic gas undergoes adiabatic process. Its volume and temperature are related as TVP = constant. The value of p will be
(1)1.33(2)1.67(3)0.67(4)0.33
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View SolutionProve that the pressure and the volume of a degenerate electron gas are related by an equation similar to the Poisson equation, and find the adiabatic index γ=Cp/Cv.
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
<
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume
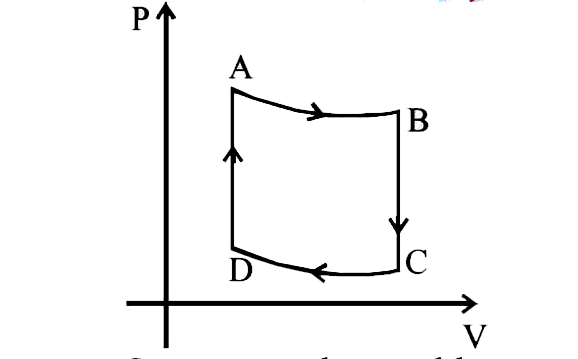
The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
View Solution