In a given process on an ideal gas, dW = 0 and dQ<0. Then for the gas
the temperature will decrease
the volume will increases
the pressure will remain constant
the temperature will increase
The correct Answer is:A
To solve the problem, we need to analyze the given conditions for an ideal gas and apply the first law of thermodynamics.
1. Understanding the Given Conditions:
- We are given that dW=0 (work done is zero).
- We also have dQ<0 (heat added to the system is negative, meaning heat is removed).
2. Applying the First Law of Thermodynamics:
- The first law of thermodynamics states:
dQ=dU+dW
- Since dW=0, we can simplify this to:
dQ=dU
3. Analyzing the Sign of dU:
- Given that dQ<0, it follows that:
dU<0
- This means that the internal energy of the gas is decreasing.
4. Relating Internal Energy to Temperature:
- For an ideal gas, the change in internal energy is related to the change in temperature by the equation:
dU=nCvdT
- Here, n is the number of moles and Cv is the specific heat at constant volume, which is a positive constant.
5. Determining the Change in Temperature:
- Since dU<0 and nCv is positive, it follows that:
dT<0
- This indicates that the temperature of the gas is decreasing.
6. Conclusion:
- Based on the analysis, since the internal energy is decreasing, the temperature of the gas must also decrease. Therefore, the correct option is:
- Option A: The temperature will decrease.
- We are given that dW=0 (work done is zero).
- We also have dQ<0 (heat added to the system is negative, meaning heat is removed).
- The first law of thermodynamics states:
dQ=dU+dW
- Since dW=0, we can simplify this to:
dQ=dU
- Given that dQ<0, it follows that:
dU<0
- This means that the internal energy of the gas is decreasing.
- For an ideal gas, the change in internal energy is related to the change in temperature by the equation:
dU=nCvdT
- Here, n is the number of moles and Cv is the specific heat at constant volume, which is a positive constant.
- Since dU<0 and nCv is positive, it follows that:
dT<0
- This indicates that the temperature of the gas is decreasing.
- Based on the analysis, since the internal energy is decreasing, the temperature of the gas must also decrease. Therefore, the correct option is:
- Option A: The temperature will decrease.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - THERMAL CONDUCTION
17 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - THERMAL RADIATION
13 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (CALORIMETRY, CHANGE OF STATE & KINETIC THEORY OF GASES )
30 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
In a given process on an ideal gas, dW=0 and dQ is negative, then for the gas:
View SolutionIn an isothermal process for an ideal gas
View SolutionDuring the process AB of an ideal gas

View SolutionDuring the process AB of an ideal gas

View SolutionIn a thermodynamic process on an ideal diatomic gas, work done by the gas is η times the heat supplied (η<1). The molar heat capacity of the gas for the process is
View SolutionCan a process on an ideal gas be both adiabatic and isothermal. ?
View SolutionIn a isothermal process on an ideal gas, the pressure increases by 0.5% . The volume decreases by about.
View SolutionIn isobaric process of ideal gas (f=5) work done by gas is equal of 10J. Then heat given to gas during process:
View SolutionThe figures given below show different processes (relating pressure P and volume V) for a given amount of an ideal gas. W is work done by the gas and ΔQ is heat absorbed by the gas.
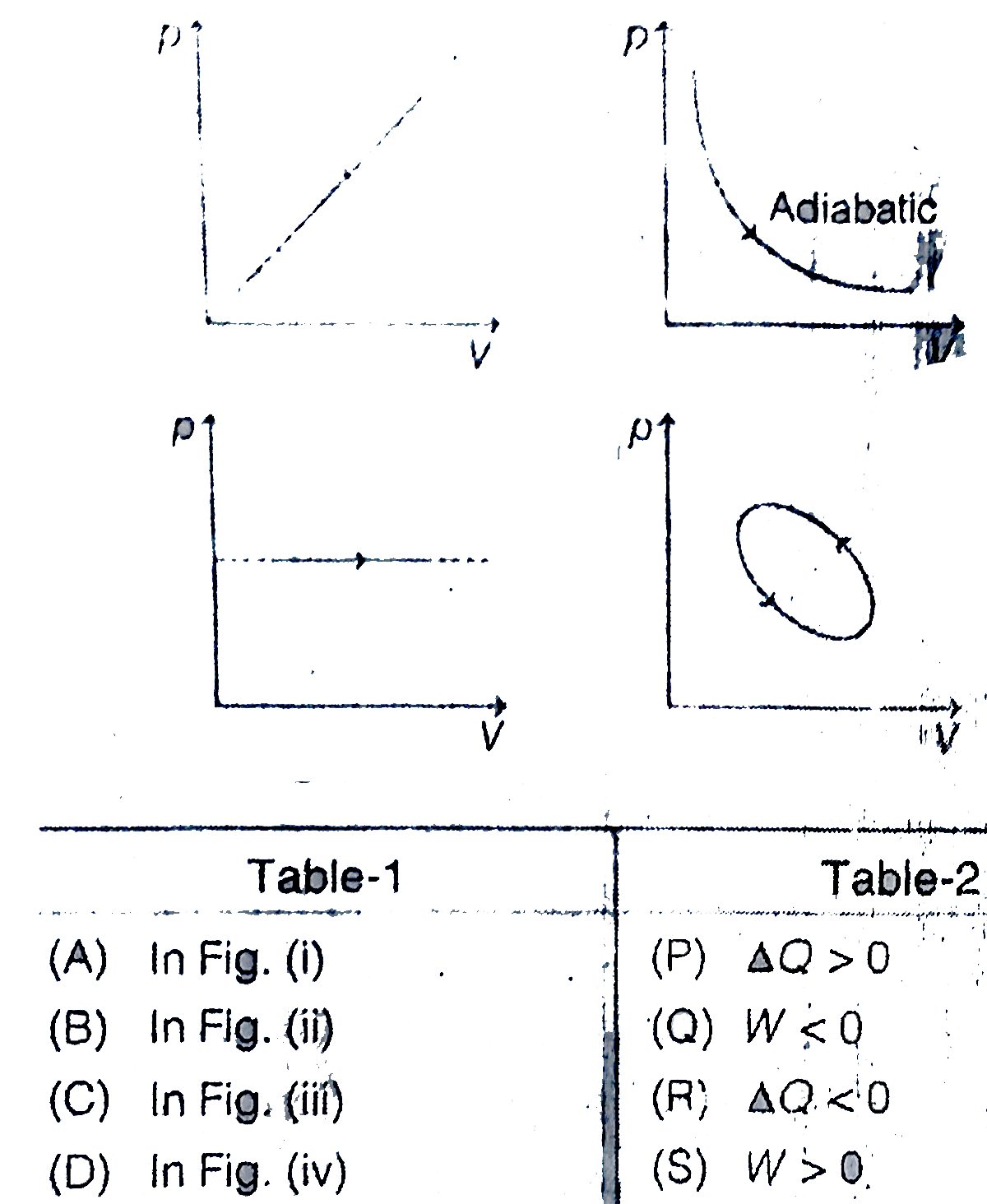
View SolutionShow that in an isothermal expansion of an ideal gas, a ΔU=0 and b. ΔH=0.
View Solution
