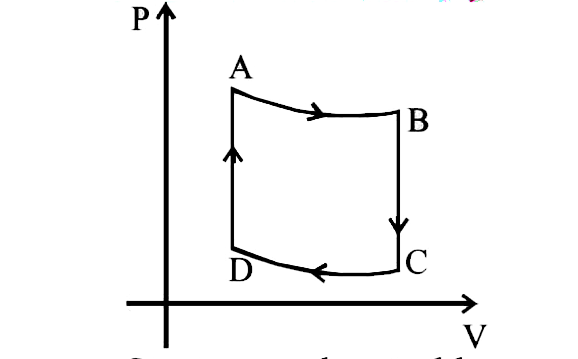
One mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
The correct Answer is:A, B
To solve the given problem step by step, we will break it down into two parts as per the question requirements:
Part (a): Work Done by the Gas in the Process A to B
1. Identify the Process: The process from A to B is an adiabatic expansion. For an adiabatic process, the work done W can be calculated using the formula:
W=P2V2−P1V1γ−1
where P1 and P2 are the pressures at states A and B, V1 and V2 are the volumes at states A and B, and γ is the heat capacity ratio.
2. Use the Ideal Gas Law: Since we do not have the volumes directly, we can use the ideal gas law PV=nRT to express the volumes in terms of pressure and temperature:
V=nRTP
Thus,
VA=nRTAPA,VB=nRTBPB
3. Calculate the Pressures: We know that:
- TA=1000K
- PB=23PA
4. Calculate the Temperature at B: Using the adiabatic relation P1Vγ1=P2Vγ2:
PA(nRTAPA)γ=PB(nRTBPB)γ
This simplifies to:
TγAP1−γA=TγBP1−γB
We can solve for TB using the ratio of pressures:
TB=TA(PBPA)γ−1γ=1000(23)25≈850K
5. Calculate Work Done: Now substituting the values back into the work done formula:
W=PBVB−PAVAγ−1
Using VA and VB from the ideal gas law:
W=(23PA⋅nR⋅85023PA)−(PA⋅nR⋅1000PA)53−1
Simplifying this gives:
W=nR(850−1000)23=nR(−150)23=−225nR
For n=1 mole and R=8.31J/(mol⋅K):
W=−225⋅8.31≈−1875J
Since work done by the gas is positive during expansion, we take the absolute value:
W≈1875J
Part (b): Heat Lost by the Gas in the Process B to C
1. Identify the Process: The process from B to C is a cooling at constant volume (isochoric process). The heat lost Q can be calculated using:
Q=nCvΔT
where Cv is the molar heat capacity at constant volume.
2. Calculate Cv: For a monoatomic ideal gas:
Cv=32R
3. Determine the Temperature Change: We need to find TC:
Using the relation for constant volume:
PBTB=PCTC
Given PC=13PA and substituting PB=23PA:
TC=TB⋅PCPB=850⋅1/32/3=850⋅12=425K
4. Calculate ΔT:
ΔT=TC−TB=425−850=−425K
5. Calculate Heat Lost:
Q=nCvΔT=1⋅32R⋅(−425)
Substituting R=8.31:
Q=32⋅8.31⋅(−425)≈−5312.25J
The heat lost is approximately 5312.25J.
Summary of Results:
- (a) Work done by the gas in the process A to B: 1875J
- (b) Heat lost by the gas in the process B to C: 5312.25J
W=P2V2−P1V1γ−1
where P1 and P2 are the pressures at states A and B, V1 and V2 are the volumes at states A and B, and γ is the heat capacity ratio.
V=nRTP
Thus,
VA=nRTAPA,VB=nRTBPB
- TA=1000K
- PB=23PA
PA(nRTAPA)γ=PB(nRTBPB)γ
This simplifies to:
TγAP1−γA=TγBP1−γB
We can solve for TB using the ratio of pressures:
TB=TA(PBPA)γ−1γ=1000(23)25≈850K
W=PBVB−PAVAγ−1
Using VA and VB from the ideal gas law:
W=(23PA⋅nR⋅85023PA)−(PA⋅nR⋅1000PA)53−1
Simplifying this gives:
W=nR(850−1000)23=nR(−150)23=−225nR
For n=1 mole and R=8.31J/(mol⋅K):
W=−225⋅8.31≈−1875J
Since work done by the gas is positive during expansion, we take the absolute value:
W≈1875J
Q=nCvΔT
where Cv is the molar heat capacity at constant volume.
Cv=32R
Using the relation for constant volume:
PBTB=PCTC
Given PC=13PA and substituting PB=23PA:
TC=TB⋅PCPB=850⋅1/32/3=850⋅12=425K
ΔT=TC−TB=425−850=−425K
Q=nCvΔT=1⋅32R⋅(−425)
Substituting R=8.31:
Q=32⋅8.31⋅(−425)≈−5312.25J
The heat lost is approximately 5312.25J.
- (a) Work done by the gas in the process A to B: 1875J
- (b) Heat lost by the gas in the process B to C: 5312.25J
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Exercise 21.11videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Exercise 21.27videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 31videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions10videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
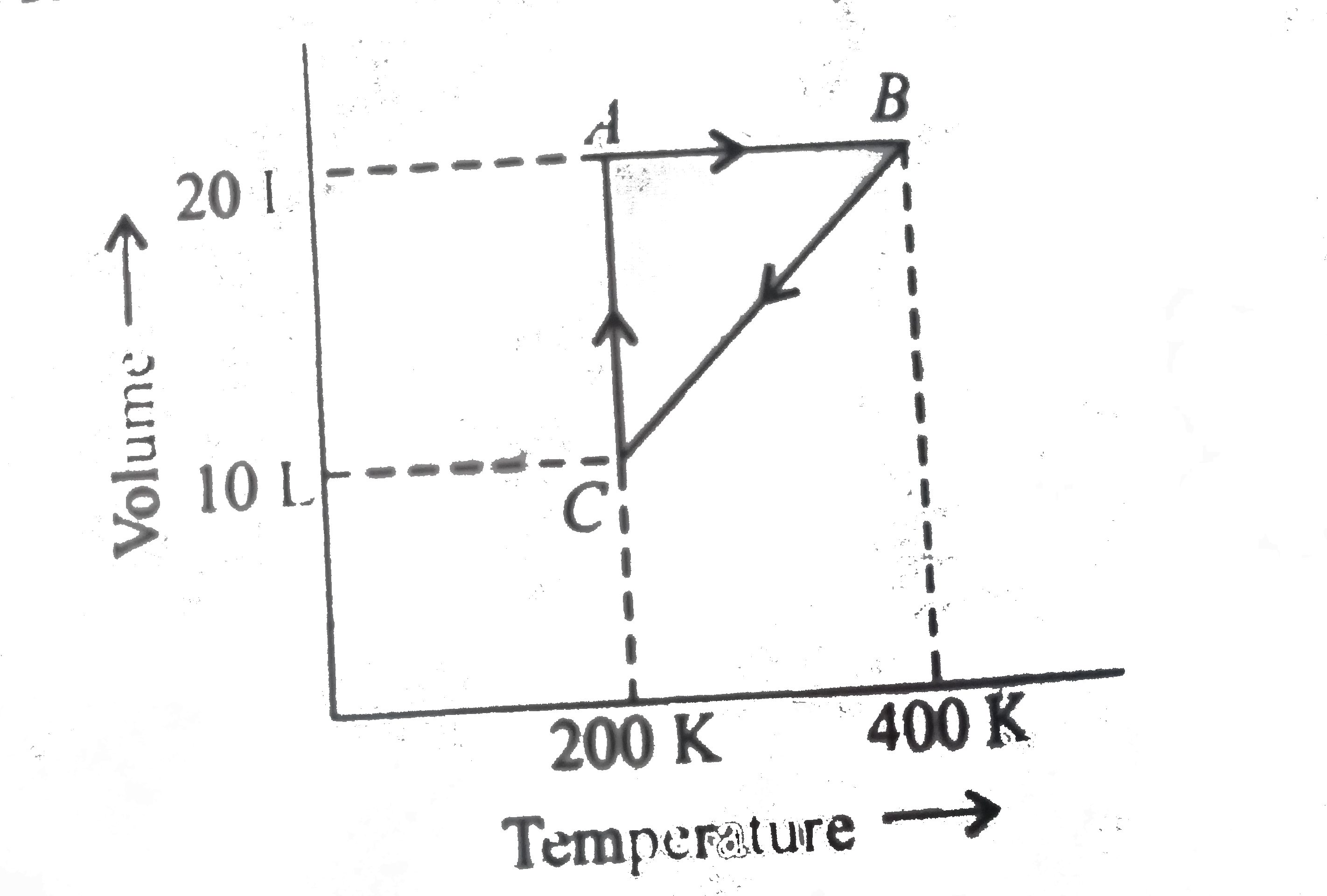
On mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
< View Solution
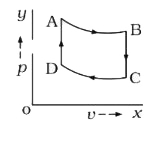
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume
The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]View Solution
Knowledge Check
- Question 1 - Select One
One mole of a monatomic ideal gas is taken through the cycle shown in figure
 The pressures and temperatures at A,B etc, are denoted by PA,TA,PB,TBetc respectively.Given TA=1000K,PB=(2/3)PAandPC=(1/3)PA Then choose the incorrect option. AThe work done by the gas in the process A→B is 1869.75JBThe heat lost by the gas sin the process B→C is -5297.25JCTemperature TD is 500KDWork done from B→C is 40J
The pressures and temperatures at A,B etc, are denoted by PA,TA,PB,TBetc respectively.Given TA=1000K,PB=(2/3)PAandPC=(1/3)PA Then choose the incorrect option. AThe work done by the gas in the process A→B is 1869.75JBThe heat lost by the gas sin the process B→C is -5297.25JCTemperature TD is 500KDWork done from B→C is 40J
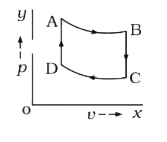
The pressure at C isView SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
B→C: cooling at constant volume
C→D adiabatic compression D→A: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The temperature TD (in K) [Given : (25)2/5=0.85 ]View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure The pressure and temperature at A, B etc are denoted by PA,PB,TA,TB−, etc respectively
A → B adiabatic expansion
B → C cooling at constant volume
C→D adiabatic compression
D→A heating at constant volume
Given that : TA=1000 K, PB=23PA and PC=13PA
_E01_271_Q01.png)
the work done by the gas in process A → BView SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure The pressure and temperature at A, B etc are denoted by PA,PB−,TA,TB−, etc respectively
A → B adiabatic expansion
B → C cooling at constant volume
C→D adiabatic compression
D→A heating at constant volume
Given that : TA=1000 K, PB=23PA and PC=13PA
_E01_271_Q01.png)
the heat lost by the gas in process B→CView SolutionOne mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC

[Assume(23)0.4=0.85 and R=253JK−1mol−1]
Heat lost by the gas in the process B→C isView SolutionOne mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
[Assume(23)0.4=0.85 and R=253JK−1mol−1]
The temperature at B is
TA=1000K and 2pA=3pB=6pC
 View Solution
View Solution
