If a block moving up at θ=30∘ with a velocity 5m/s, stops after 0.5 sec, then what is μ
0.5
1.25
0.6
None of the above
The correct Answer is:c
To solve the problem, we need to find the coefficient of friction (μ) for a block moving up an incline at an angle of θ = 30° with an initial velocity of 5 m/s, which stops after 0.5 seconds.
1. Identify the Forces Acting on the Block:
- The block experiences gravitational force acting downwards, which can be resolved into two components:
- Parallel to the incline: Fgravity, parallel=mgsinθ
- Perpendicular to the incline: Fgravity, perpendicular=mgcosθ
2. Determine the Normal Force (N):
- The normal force acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ
3. Frictional Force (F_f):
- The frictional force acting on the block is given by:
Ff=μN=μ(mgcosθ)
4. Apply Newton's Second Law:
- According to Newton's second law, the net force acting on the block is equal to the mass times its acceleration (a):
Ff+mgsinθ=ma
- Substituting the expressions for frictional force and gravitational force:
μ(mgcosθ)+mgsinθ=ma
5. Cancel the Mass (m):
- Since mass (m) appears in every term, we can cancel it out:
μgcosθ+gsinθ=a
6. Calculate the Acceleration (a):
- The acceleration can be calculated using the formula:
a=vf−vit
- Here, vf=0 m/s (final velocity), vi=5 m/s (initial velocity), and t=0.5 s:
a=0−50.5=−10m/s2
7. Substitute the Acceleration into the Equation:
- Now, substituting a=−10 m/s² into the equation:
−10=μgcosθ+gsinθ
8. Use Values for g, sin(30°), and cos(30°):
- We know g≈10m/s2, sin(30°)=12, and cos(30°)=√32:
−10=μ(10)(√32)+(10)(12)
- Simplifying:
−10=5√3μ+5
9. Rearranging the Equation:
- Move the constant term to the other side:
−10−5=5√3μ
−15=5√3μ
10. Solve for μ:
- Divide both sides by 5√3:
μ=−155√3=−3√3=−√3
- Since we are looking for the magnitude of the coefficient of friction, we take the positive value:
μ=1√3≈0.577≈0.6
Conclusion:
The coefficient of friction μ is approximately 0.6. Thus, the correct answer is option C.
- The block experiences gravitational force acting downwards, which can be resolved into two components:
- Parallel to the incline: Fgravity, parallel=mgsinθ
- Perpendicular to the incline: Fgravity, perpendicular=mgcosθ
- The normal force acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ
- The frictional force acting on the block is given by:
Ff=μN=μ(mgcosθ)
- According to Newton's second law, the net force acting on the block is equal to the mass times its acceleration (a):
Ff+mgsinθ=ma
- Substituting the expressions for frictional force and gravitational force:
μ(mgcosθ)+mgsinθ=ma
- Since mass (m) appears in every term, we can cancel it out:
μgcosθ+gsinθ=a
- The acceleration can be calculated using the formula:
a=vf−vit
- Here, vf=0 m/s (final velocity), vi=5 m/s (initial velocity), and t=0.5 s:
a=0−50.5=−10m/s2
- Now, substituting a=−10 m/s² into the equation:
−10=μgcosθ+gsinθ
- We know g≈10m/s2, sin(30°)=12, and cos(30°)=√32:
−10=μ(10)(√32)+(10)(12)
- Simplifying:
−10=5√3μ+5
- Move the constant term to the other side:
−10−5=5√3μ
−15=5√3μ
- Divide both sides by 5√3:
μ=−155√3=−3√3=−√3
- Since we are looking for the magnitude of the coefficient of friction, we take the positive value:
μ=1√3≈0.577≈0.6
The coefficient of friction μ is approximately 0.6. Thus, the correct answer is option C.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - MOTION IN FLUIDS
25 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION
25 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( WORK POWER ENERGY )
35 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
In the block moves up with constant velocity v m/s. Find F

View SolutionA turck is moving on the ground with a velocity v=12m/s and a box is moving on the truck with respect to it with a velocity u=5m/s as shown in the figure. What is the velocity of the box with respect to the ground?

View Solution
Knowledge Check
A particle moves in the direction of east for 2s with velocity of 15m/s .Then it moves towards north for 8s with a velocity of 5m/s . The average velocity of the particle is (in m/s)
A1 m/sB5 m/sC7 m/sD10 m/s
A block slides on ice with a velocity of 5m/s comes to rest after moving through a distance of 13.5m . Find the coefficient of friction ?
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA block of mass 0.5 kg is kept on a rough inclined plane making an angle of 30∘ with horizontal. What power will be required to move the block up the plane (along the plane) with a velocity of 5m/s ? (Take m = 0.2 between block and plane)
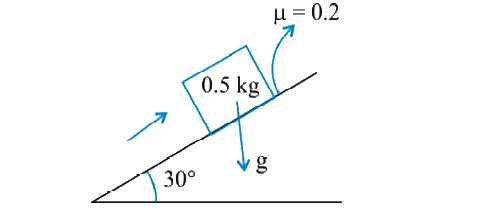
View SolutionA particle is moving eastwards with velocity of 5m/s. In 10sec the velocity changes to 5m/s northwards. The average acceleration in this time is.
View SolutionA motor is fixed inside a box which is moving upwards with velocity 5m/s. String is winding at the rate 3m/s Then the velocity of block A will be.
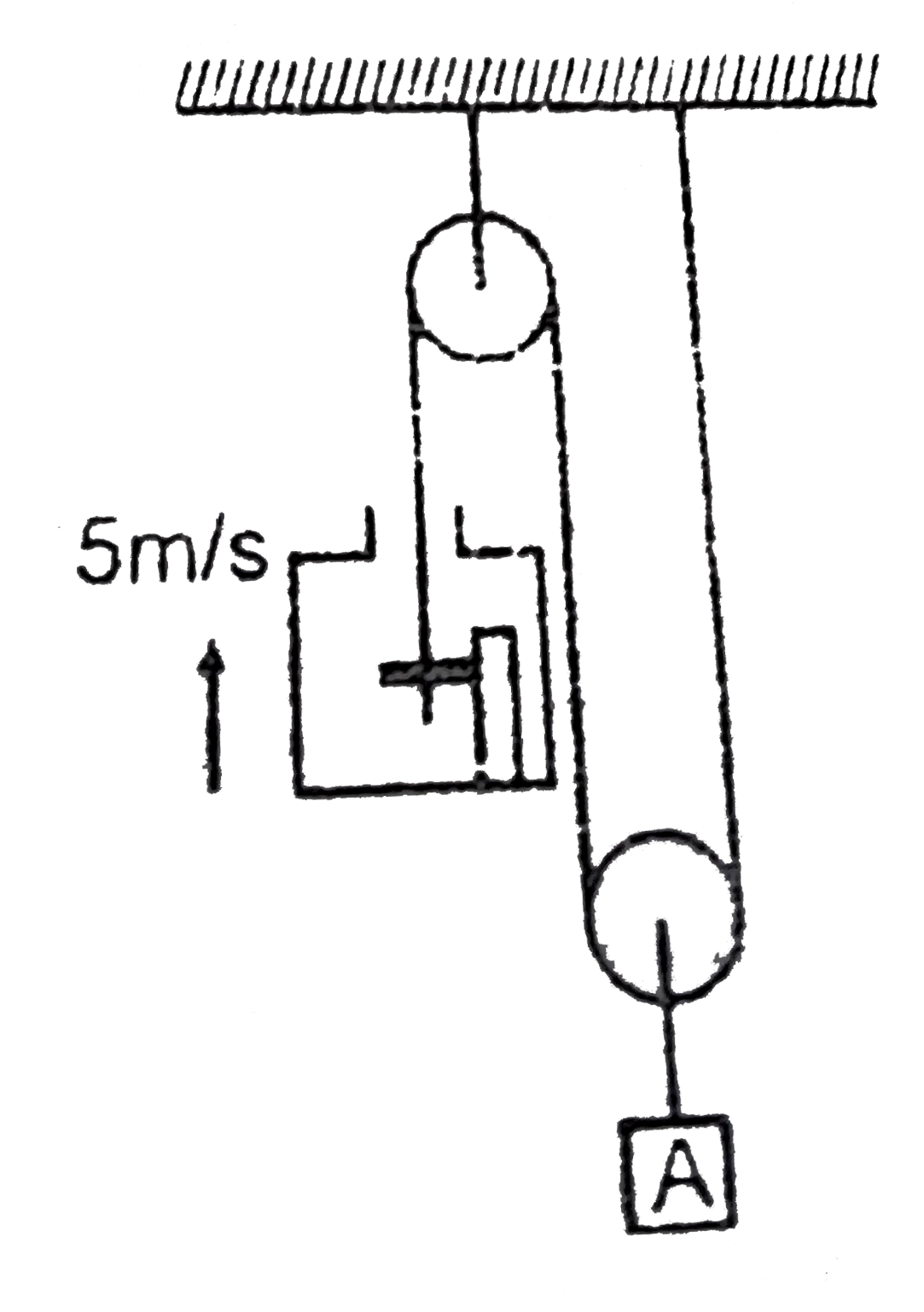
View SolutionA block starts going up a rough inclined plane with velocity V0 as shown in figure.After some time reaches to starting point again, with a velocity V02.Find coefficient of friction μ .Given g=10msec2.
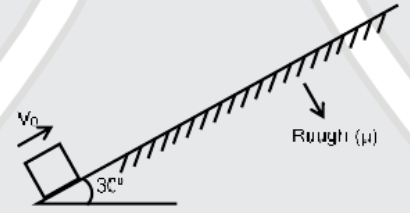
View Solution
