A weightless rod is acted upon by upward parallel forces of 2 newton and 4 newton magnitudes at ends A and B respectively. The total length of the rod AB = 3metere. TO keep the rod in equilibrium a force of 6 newton act in the following manner.
downward at any point between A and B
downward at the mid-point of AB
downward at a point C such that AC = 1 metre
downward at a point D such that BD = 1 metre
The correct Answer is:d
To solve the problem step by step, we need to analyze the forces acting on the rod and apply the conditions for equilibrium.
Step 1: Identify the Forces Acting on the Rod
- At point A, there is an upward force of 2 N.
- At point B, there is an upward force of 4 N.
- To maintain equilibrium, we need to introduce a downward force of 6 N.
Step 2: Set Up the Equilibrium Conditions
For the rod to be in equilibrium, the net force and net torque acting on it must both be zero.
1. Net Force Condition:
Fup−Fdown=0
Here, Fup=2N+4N=6N and Fdown=6N. Thus, the net force is zero.
2. Net Torque Condition:
We can take moments about point A or point B. Here, we will take moments about point A.
Step 3: Calculate the Torque About Point A
- The torque due to the 4 N force at point B (which is 3 m from A):
τB=4N×3m=12N m(clockwise)
- The torque due to the 6 N force (let's say it is at a distance x from point B, which means it is 3−x from point A):
τ6N=6N×(3−x)m(counterclockwise)
Step 4: Set Up the Torque Equation
For equilibrium, the sum of the torques about point A must be zero:
τ6N−τB=0
Substituting the values:
6(3−x)−12=0
Step 5: Solve for x
Expanding the equation:
18−6x−12=0
6−6x=0
6x=6⟹x=1m
Step 6: Determine the Position of the 6 N Force
Since x=1m is the distance from point B, the distance from point A is:
3−x=3−1=2m
Conclusion
The 6 N force acts downward at a point that is 1 meter from B and 2 meters from A. Therefore, the correct answer is that the force acts downward at point D such that BD = 1 meter.
- At point A, there is an upward force of 2 N.
- At point B, there is an upward force of 4 N.
- To maintain equilibrium, we need to introduce a downward force of 6 N.
For the rod to be in equilibrium, the net force and net torque acting on it must both be zero.
Fup−Fdown=0
Here, Fup=2N+4N=6N and Fdown=6N. Thus, the net force is zero.
We can take moments about point A or point B. Here, we will take moments about point A.
- The torque due to the 4 N force at point B (which is 3 m from A):
τB=4N×3m=12N m(clockwise)
- The torque due to the 6 N force (let's say it is at a distance x from point B, which means it is 3−x from point A):
τ6N=6N×(3−x)m(counterclockwise)
For equilibrium, the sum of the torques about point A must be zero:
τ6N−τB=0
Substituting the values:
6(3−x)−12=0
Expanding the equation:
18−6x−12=0
6−6x=0
6x=6⟹x=1m
Since x=1m is the distance from point B, the distance from point A is:
3−x=3−1=2m
The 6 N force acts downward at a point that is 1 meter from B and 2 meters from A. Therefore, the correct answer is that the force acts downward at point D such that BD = 1 meter.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( WORK POWER ENERGY )
Explore 35 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:FRICTION
Explore 22 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (PROJECTILE MOTION)
Explore 31 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
A weightless rod is acted upon by two upward parallel forces of 2N and 4N at ends A and B respectively. The total length of the rod AB=3m. To keep the rod in equilibrium a force of 6N should act in the following manner.
View SolutionTwo like parallel force 20 N and 30 N act at the ands A and B of a rod 1.5 m long. The resultant of the forces will act at the point
View Solution
Knowledge Check
A rigid rod of length 2L is acted upon by some forces. All forces labelled F have the same magnitude. Which cases have a non-zero net torque acting on the rod about its centre ?
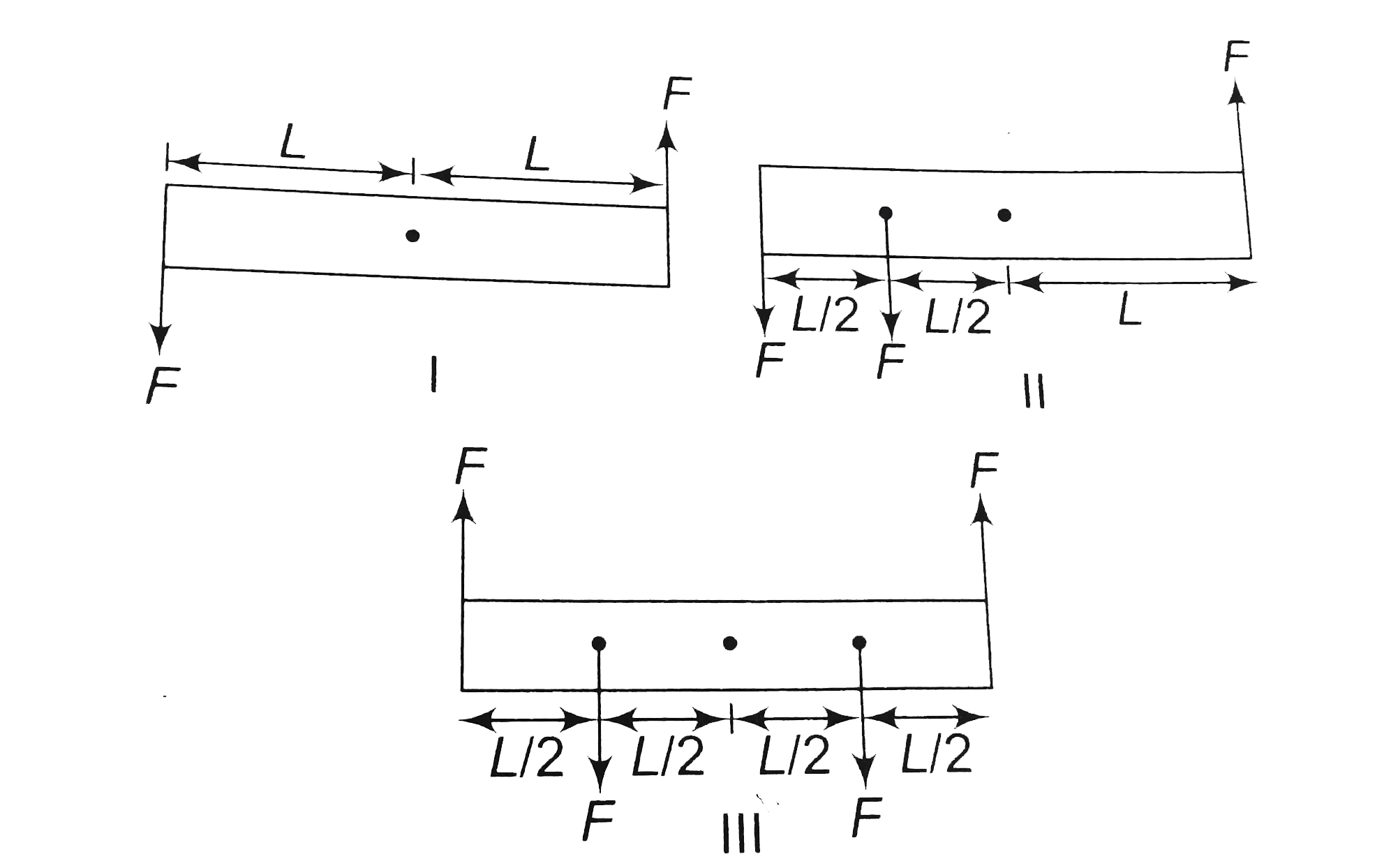 .AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.
.AI and II onlyBII and III onlyCI and III onlyDThe net torque is zero in all cases.A body of mass 2kg is acted by two forces each of magnitude 1 newton, making an angle of 60∘ with each other. The net acceleration of the body (inm/s2) is
A0.5B1C√3/2D√2/3
ABC is an isosceles triangle right angled at A. forces of magnitude 2√2,5and6 act along BC, CA and AB respectively. The magnitude of their resultant force is
View SolutionThree parallel forces are acting on a rod at distances of 40 cm, 60 cm and 80 cm respectively from one end of the rod (as shown in figure). Assuming no other forces, the rod under the influence of these forces will :-

View SolutionA homogeneous rod of length L is acted upon by two forces F1andF2 applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where F1 is applied?
View SolutionA long uniform rod of length L and mass M is free to rotate in a horizontal plane about a vertical axis through its one end 'O'. A spring of force constant k is connected between one end of the rod and PQ. When the rod is in equilibrium it is parallel to PQ.

(a)What is the period of small oscillation that result when the rod is rotated slightly and released ?
(b) What will be the maximum speed of the displacement end of the rod, if the amplitude of motion is θ0?
View SolutionA rod of mass m and length L , lying horizontally is free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude F acts on the rod at a distance of L/4 from the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.
View SolutionA force (3ˆi+4ˆj) newton acts on a body and displaces it by (3ˆI+4ˆj) metere. The work done by the force is y Joules. Find y.
View Solution

