The time of flight of projectile on an upward inclined plane depends upon.
angle of projection
angle of inclination of the plane
air resistance
a and b both
The correct Answer is:d
To determine the factors that affect the time of flight of a projectile on an upward inclined plane, we can follow these steps:
1. Understanding the Problem:
We have a projectile launched at an angle ϕ from an inclined plane that has an angle of inclination θ. We need to find out how the time of flight depends on the angle of projection ϕ and the angle of inclination θ.
2. Setting Up the Coordinate System:
We will set up a coordinate system where the x-axis is along the incline and the y-axis is perpendicular to the incline. This simplifies our calculations.
3. Breaking Down the Initial Velocity:
The initial velocity u of the projectile can be broken down into its components:
- The component along the incline (x-direction):
ux=ucosϕ
- The component perpendicular to the incline (y-direction):
uy=usinϕ
4. Identifying the Effect of Gravity:
The acceleration due to gravity g acts downwards. We need to find its components along the inclined plane:
- The component of gravity acting down the incline (x-direction):
gx=gsinθ
- The component of gravity acting perpendicular to the incline (y-direction):
gy=gcosθ
5. Using the Time of Flight Formula:
The time of flight T for a projectile is given by the formula:
T=2uygy
Substituting our values for uy and gy:
T=2(usinϕ)gcosθ
6. Analyzing the Result:
From the equation T=2usinϕgcosθ, we can see that:
- The time of flight T is directly proportional to sinϕ (angle of projection).
- The time of flight T is inversely proportional to cosθ (angle of inclination).
7. Conclusion:
Therefore, the time of flight of a projectile on an upward inclined plane depends on both the angle of projection ϕ and the angle of inclination θ.
Final Answer:
The time of flight of a projectile on an upward inclined plane depends on both the angle of projection ϕ and the angle of inclination θ.
We have a projectile launched at an angle ϕ from an inclined plane that has an angle of inclination θ. We need to find out how the time of flight depends on the angle of projection ϕ and the angle of inclination θ.
We will set up a coordinate system where the x-axis is along the incline and the y-axis is perpendicular to the incline. This simplifies our calculations.
The initial velocity u of the projectile can be broken down into its components:
- The component along the incline (x-direction):
ux=ucosϕ
- The component perpendicular to the incline (y-direction):
uy=usinϕ
The acceleration due to gravity g acts downwards. We need to find its components along the inclined plane:
- The component of gravity acting down the incline (x-direction):
gx=gsinθ
- The component of gravity acting perpendicular to the incline (y-direction):
gy=gcosθ
The time of flight T for a projectile is given by the formula:
T=2uygy
Substituting our values for uy and gy:
T=2(usinϕ)gcosθ
From the equation T=2usinϕgcosθ, we can see that:
- The time of flight T is directly proportional to sinϕ (angle of projection).
- The time of flight T is inversely proportional to cosθ (angle of inclination).
Therefore, the time of flight of a projectile on an upward inclined plane depends on both the angle of projection ϕ and the angle of inclination θ.
The time of flight of a projectile on an upward inclined plane depends on both the angle of projection ϕ and the angle of inclination θ.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( Laws of motion )
Explore 36 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( WORK POWER ENERGY )
Explore 35 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (UNIFORMLY ACCELERATED MOTION)
Explore 58 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
The time of flight of the projectile is:
View SolutionIn the figure shown, find.
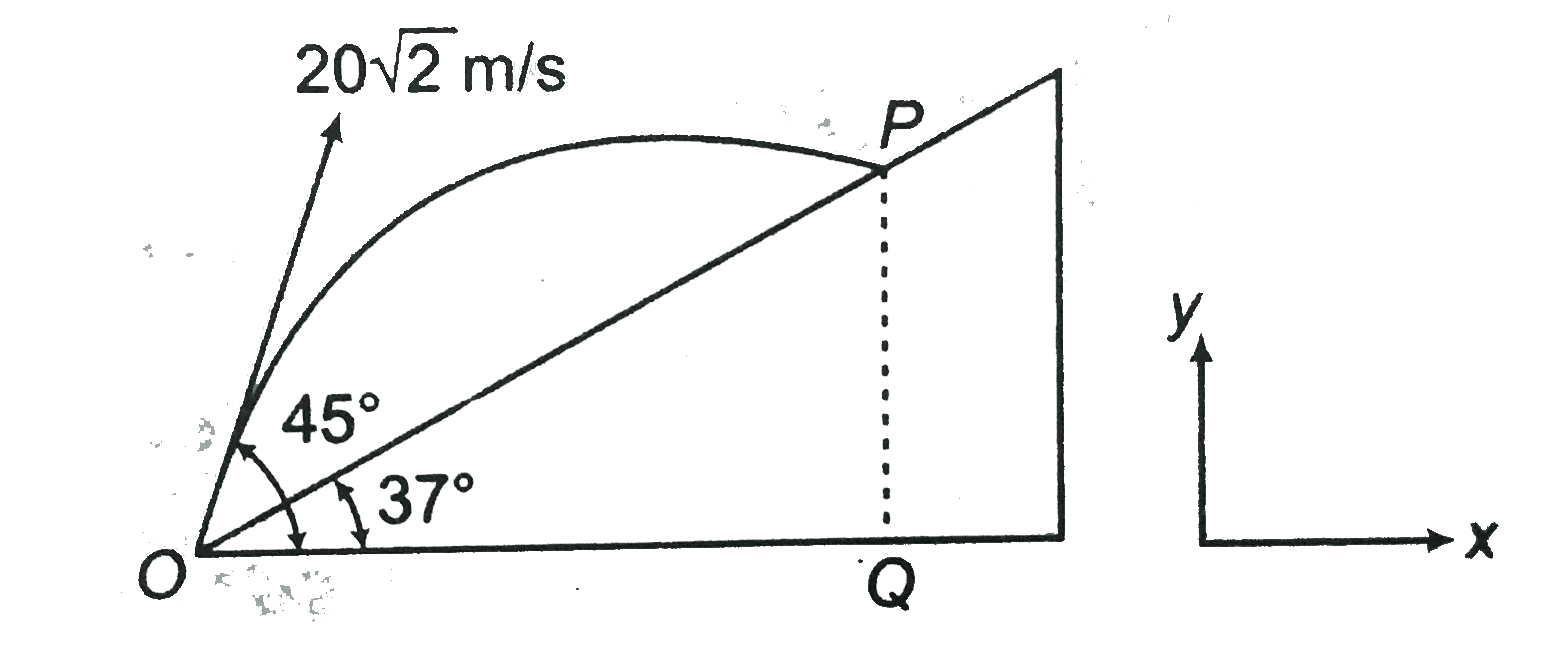
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
View SolutionIn the figure shown, find.
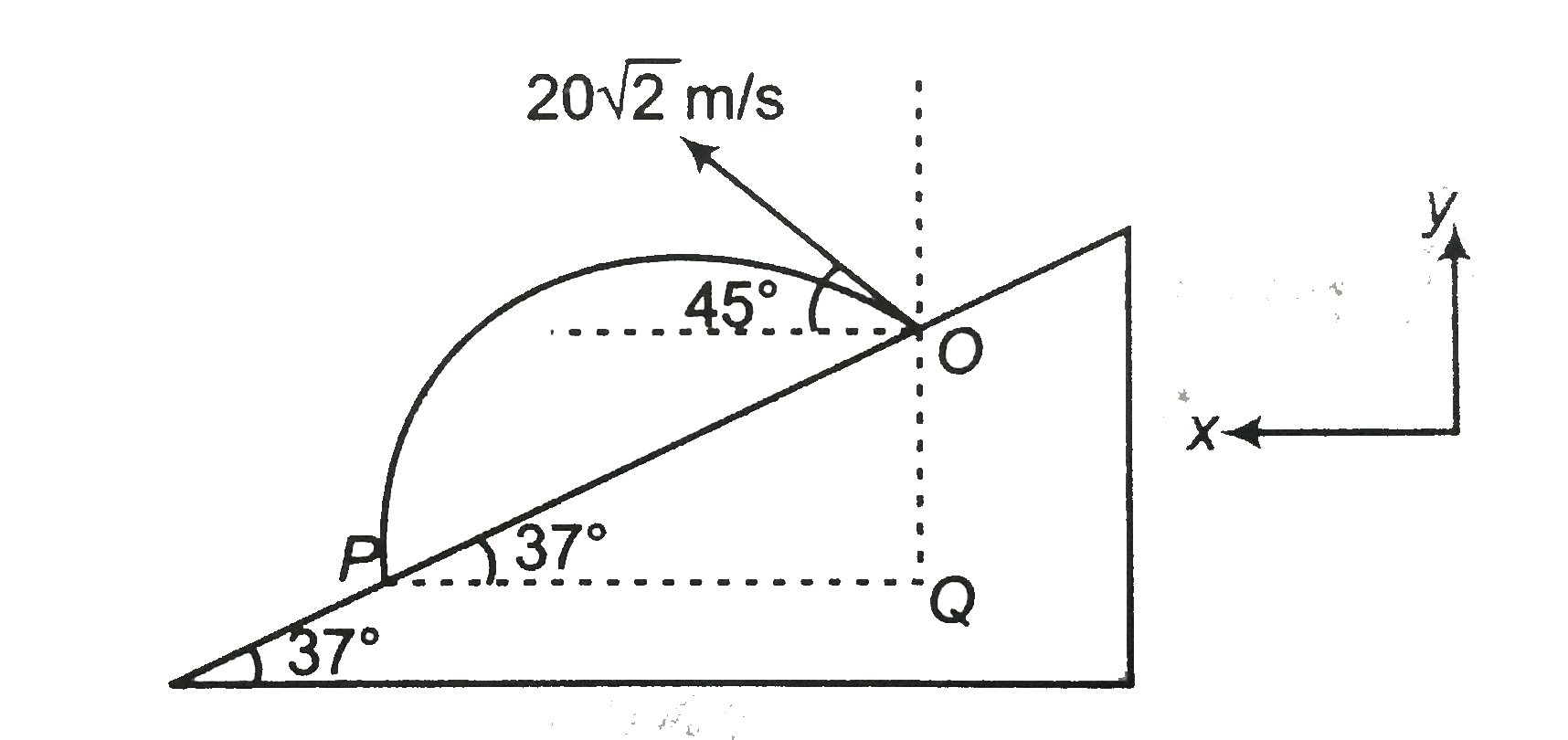
(a) time of flight of the projectile along the inclined plane.
(b) range OP.
View SolutionAdsorption depends upon
View SolutionIn the figure shown, find
 .
.
(a) the time of flight of the projectile over the inciled plane.
(b) range OP.
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
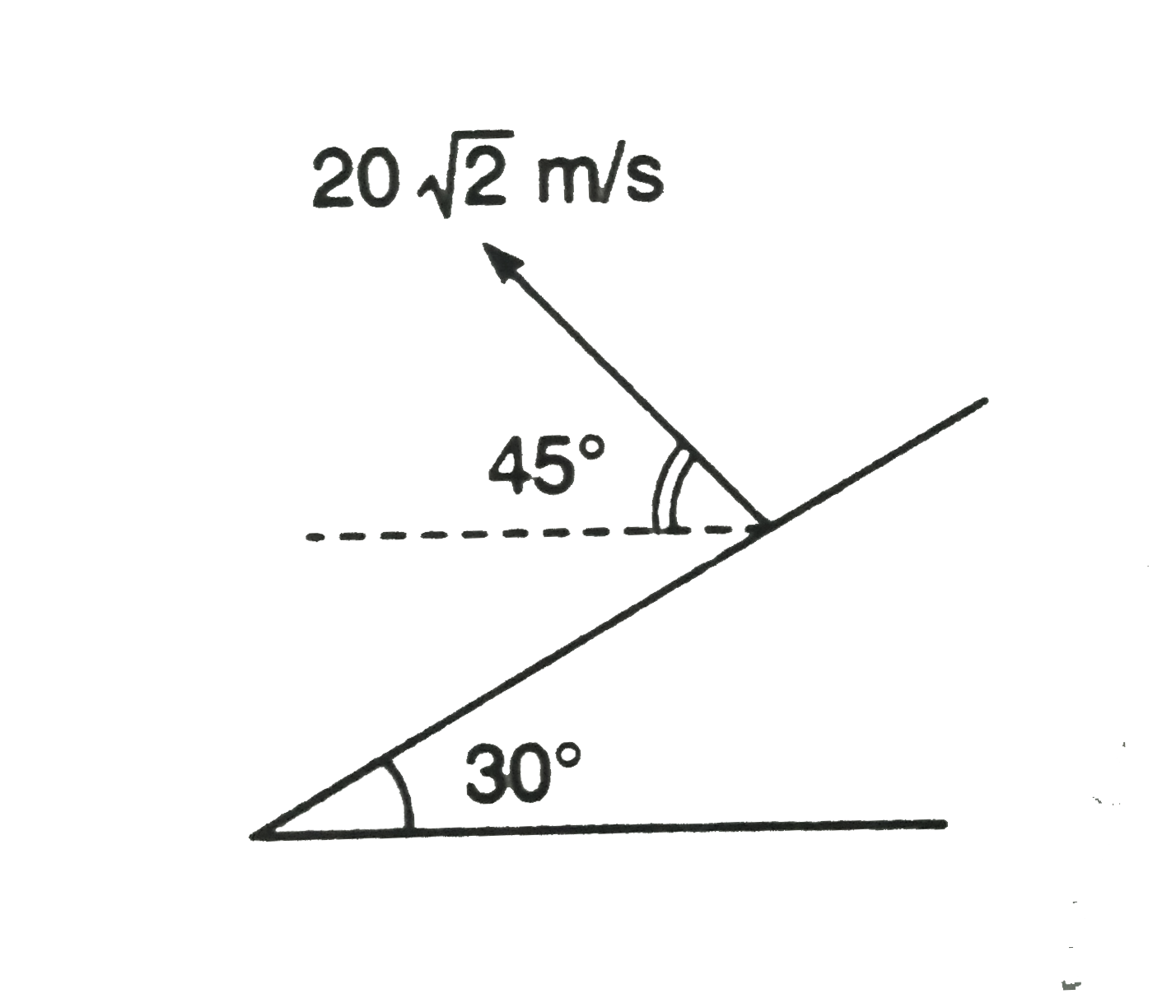
View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)

View SolutionFind time of flight and range of the projectile along the inclined plane as shown in figure. (g=10m/s2)
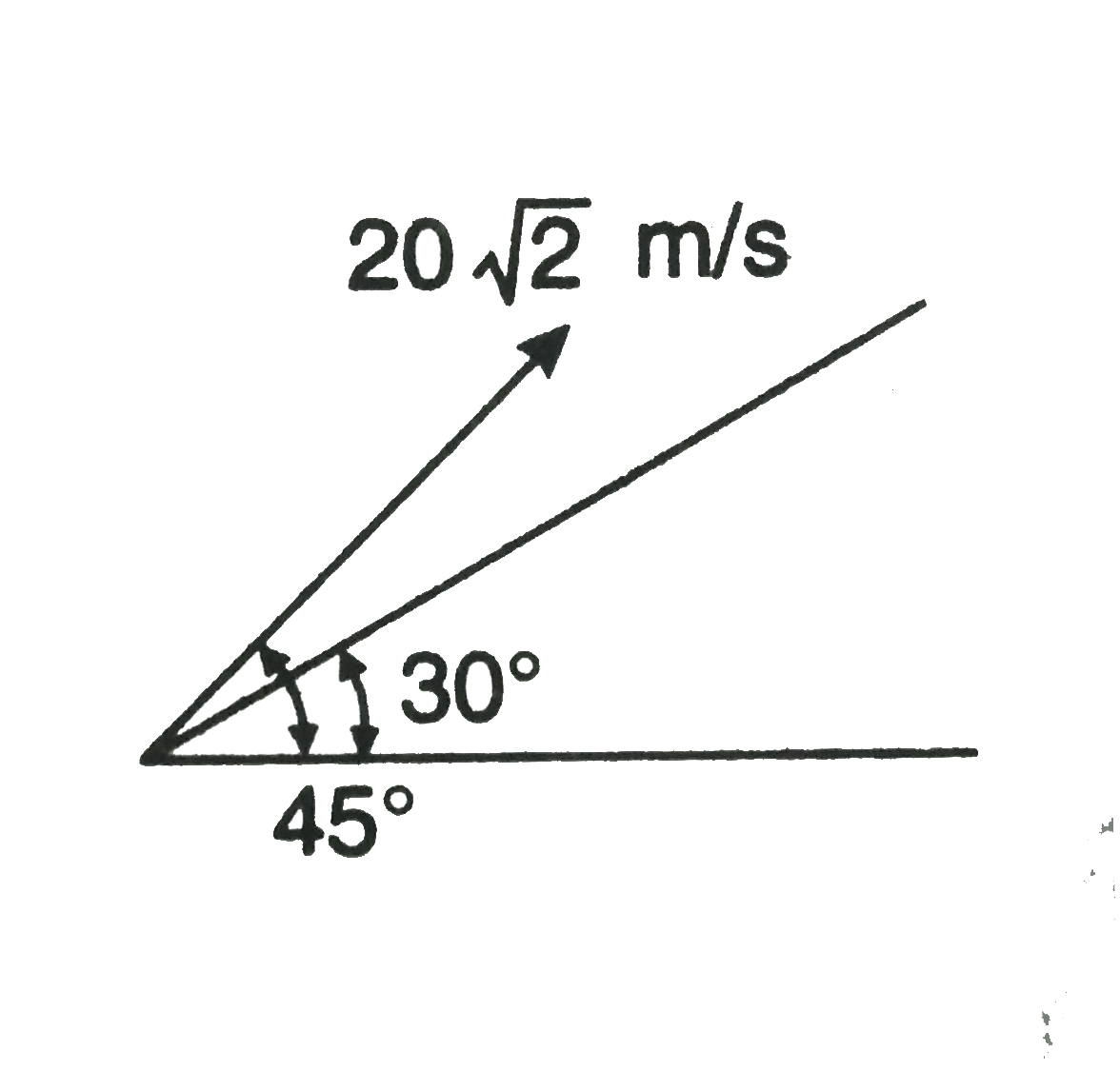
View Solution(A) : The time of ascent for a body projected to move up a rough inclined plane is less than the time of descent.
(R ) : The retardation for upward motion is more than the acceleration for down motion on rough inclined plane.
View SolutionDispersive power depends upon
View Solution

