The velocity of projection of a body is increased by 2%. Other factors remaining unchanged, what will be the percentage change in the maximum height attained ?
0.04
0.02
0.03
0.05
The correct Answer is:a
To solve the problem, we need to determine the percentage change in the maximum height attained by a projectile when the velocity of projection is increased by 2%.
1. Understanding the formula for maximum height:
The maximum height (H) attained by a projectile is given by the formula:
H=u2sin2θ2g
where u is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
2. Identifying the change in velocity:
We are given that the velocity of projection is increased by 2%. Therefore, if the original velocity is u, the new velocity u′ can be expressed as:
u′=u+0.02u=1.02u
3. Calculating the change in maximum height:
The new maximum height H′ with the increased velocity can be calculated as:
H′=(u′)2sin2θ2g=(1.02u)2sin2θ2g=1.0404u2sin2θ2g
4. Finding the percentage change in height:
The original maximum height H is:
H=u2sin2θ2g
The percentage change in height can be calculated using the formula:
Percentage Change=H′−HH×100
Substituting the values of H′ and H:
Percentage Change=1.0404u2sin2θ2g−u2sin2θ2gu2sin2θ2g×100
Simplifying this gives:
=1.0404−11×100=0.0404×100=4.04%
5. Conclusion:
Therefore, the percentage change in the maximum height attained is approximately 4.04%.
Final Answer:
The percentage change in the maximum height attained is 4%.
The maximum height (H) attained by a projectile is given by the formula:
H=u2sin2θ2g
where u is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
We are given that the velocity of projection is increased by 2%. Therefore, if the original velocity is u, the new velocity u′ can be expressed as:
u′=u+0.02u=1.02u
The new maximum height H′ with the increased velocity can be calculated as:
H′=(u′)2sin2θ2g=(1.02u)2sin2θ2g=1.0404u2sin2θ2g
The original maximum height H is:
H=u2sin2θ2g
The percentage change in height can be calculated using the formula:
Percentage Change=H′−HH×100
Substituting the values of H′ and H:
Percentage Change=1.0404u2sin2θ2g−u2sin2θ2gu2sin2θ2g×100
Simplifying this gives:
=1.0404−11×100=0.0404×100=4.04%
Therefore, the percentage change in the maximum height attained is approximately 4.04%.
The percentage change in the maximum height attained is 4%.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( Laws of motion )
Explore 36 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( WORK POWER ENERGY )
Explore 35 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (UNIFORMLY ACCELERATED MOTION)
Explore 58 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
If kinetic energy of a body is increased by 300%, then percentage change in momentum will be
View Solution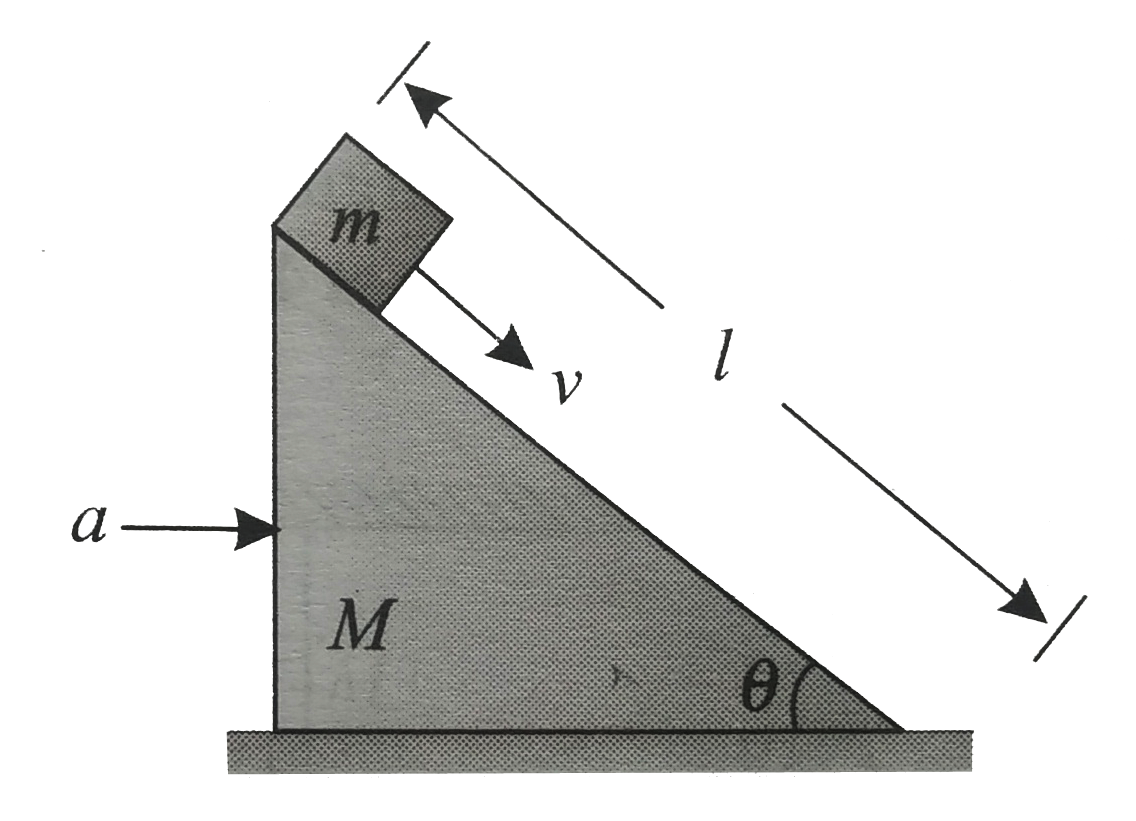
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionThe maximum height attained by a projectile is increased by 5%. Keeping the angle of projection constant, what is the percentage increases in horizontal range?
View SolutionThe operating potential in an x-ray tube is increased by 2%. The percentage change in the cut off wavelength is
View SolutionA body is projected with velocity u such that in horizontal range and maximum vertical heights are same.The maximum height is
View SolutionWhen kinetic energy of a body is increased by 800%, then percentage change in its linear momentum is
View SolutionIf length of simple pendulum is increased by 6% then percentage change in the time-period will be
View SolutionThe wire is stretched to increase the length by 1%. Find the percentage change in the resistance.
View SolutionThe maximum height attaine by a projectile is increased by 10% by increasing its speed of projecton, without changing the angle of projection. What will the percentage increase in the horizontal range.
View SolutionThe maximum height attaine by a projectile is increased by 10% by increasing its speed of projecton, without changing the angle of projection. What will the percentage increase in the horizontal range.
View Solution

