The first and the second runners in a 100 m dash have a gap of half metre at the mid way stage. By what percentage should the second runner increase his speed just to win the race, assuming that the first runner goes steady ?
0.01
0.0102
0.02
0.0202
The correct Answer is:d
To solve the problem step by step, we will analyze the situation of the two runners in the 100 m dash.
Step 1: Understand the positions of the runners at the midway point
At the midway point (50 m), the first runner (A) has covered 50 m, while the second runner (B) has covered 49.5 m. This means that B is 0.5 m behind A.
Step 2: Determine the time taken by both runners to reach the midway point
Let the speed of runner A be v1 and the speed of runner B be v2. The time taken by A to reach the midway point can be expressed as:
t=50v1
For runner B, the time taken to cover 49.5 m is:
t=49.5v2
Since both runners reach the midway point at the same time, we can equate the two expressions:
50v1=49.5v2
Step 3: Determine the time taken to finish the race
After reaching the midway point, runner A still has to cover another 50 m to finish the race. The time taken by A to cover this distance is:
tA=50v1
Runner B, who is now 0.5 m behind, needs to cover 50.5 m to finish the race. The time taken by B to cover this distance at a new speed v3 is:
tB=50.5v3
Step 4: Set the finishing times equal
For runner B to win, he must finish just before A, which means we can set the finishing times equal:
50v1=50.5v3
Step 5: Relate the speeds of the runners
From the two equations we have:
1. 50v1=49.5v2
2. 50v1=50.5v3
From the first equation, we can express v1 in terms of v2:
v1=50⋅v249.5
Substituting this into the second equation gives:
5050⋅v249.5=50.5v3
Simplifying this leads to:
49.5v2=50.5v3
Step 6: Find the new speed v3
Rearranging gives:
v3=v2⋅50.549.5
Step 7: Calculate the percentage increase in speed
The percentage increase in speed from v2 to v3 is given by:
Percentage Increase=v3−v2v2×100
Substituting v3:
Percentage Increase=v2⋅50.549.5−v2v2×100
This simplifies to:
Percentage Increase=(50.5−49.549.5)×100=149.5×100≈2.02%
Final Answer
The second runner must increase his speed by approximately 2.02% to win the race.
---
At the midway point (50 m), the first runner (A) has covered 50 m, while the second runner (B) has covered 49.5 m. This means that B is 0.5 m behind A.
Let the speed of runner A be v1 and the speed of runner B be v2. The time taken by A to reach the midway point can be expressed as:
t=50v1
For runner B, the time taken to cover 49.5 m is:
t=49.5v2
Since both runners reach the midway point at the same time, we can equate the two expressions:
50v1=49.5v2
After reaching the midway point, runner A still has to cover another 50 m to finish the race. The time taken by A to cover this distance is:
tA=50v1
Runner B, who is now 0.5 m behind, needs to cover 50.5 m to finish the race. The time taken by B to cover this distance at a new speed v3 is:
tB=50.5v3
For runner B to win, he must finish just before A, which means we can set the finishing times equal:
50v1=50.5v3
From the two equations we have:
1. 50v1=49.5v2
2. 50v1=50.5v3
v1=50⋅v249.5
5050⋅v249.5=50.5v3
Simplifying this leads to:
49.5v2=50.5v3
Rearranging gives:
v3=v2⋅50.549.5
The percentage increase in speed from v2 to v3 is given by:
Percentage Increase=v3−v2v2×100
Substituting v3:
Percentage Increase=v2⋅50.549.5−v2v2×100
This simplifies to:
Percentage Increase=(50.5−49.549.5)×100=149.5×100≈2.02%
The second runner must increase his speed by approximately 2.02% to win the race.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (PROJECTILE MOTION)
Explore 31 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( Laws of motion )
Explore 36 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:VECTORS AND SCALARS [Selected from Previoius Years Engg. & Med. & IIT Exam Qns]
Explore 35 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
Consider a two particle system with the particles having masses m1andm2. If the first particles pushed towards the centre of mass through a distance d, by what distance should the second particle be moved so as the keep the centre of mass at the same position?
View SolutionThe first order reaction has k=1.5×10−6 per second at 200∘C . If the reaction is allowed to ruf for 10 hours at the same temperature, what percentage of the initial concentration would have changed into the product? What is the half life period of this reaction ?
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends on the properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
Which object would first acquire half of their respective terminal speed in minimum time from start of the motion of all were released simultaneously ?
View SolutionTwo boys simultaenously aim their guns at a brid sitting on a tower. The first boy releases his shot with a speed of 100m/s at an angle of projection of 30∘. The second boy is ahead of the first by a distance of 50m and releases his shot with a speed of 80m/s. How must he aim his gun so that both the shots hit the bird simultaenously ? What is the distance of the foot of the tower from the first boy and the height of the tower ?
View SolutionIn a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Figure). A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run? [Hint : To pick up the first potato and the second potato, the total distance (in metres) rim by a competitor is 2 x 5 + 2 x (5 + 3)]
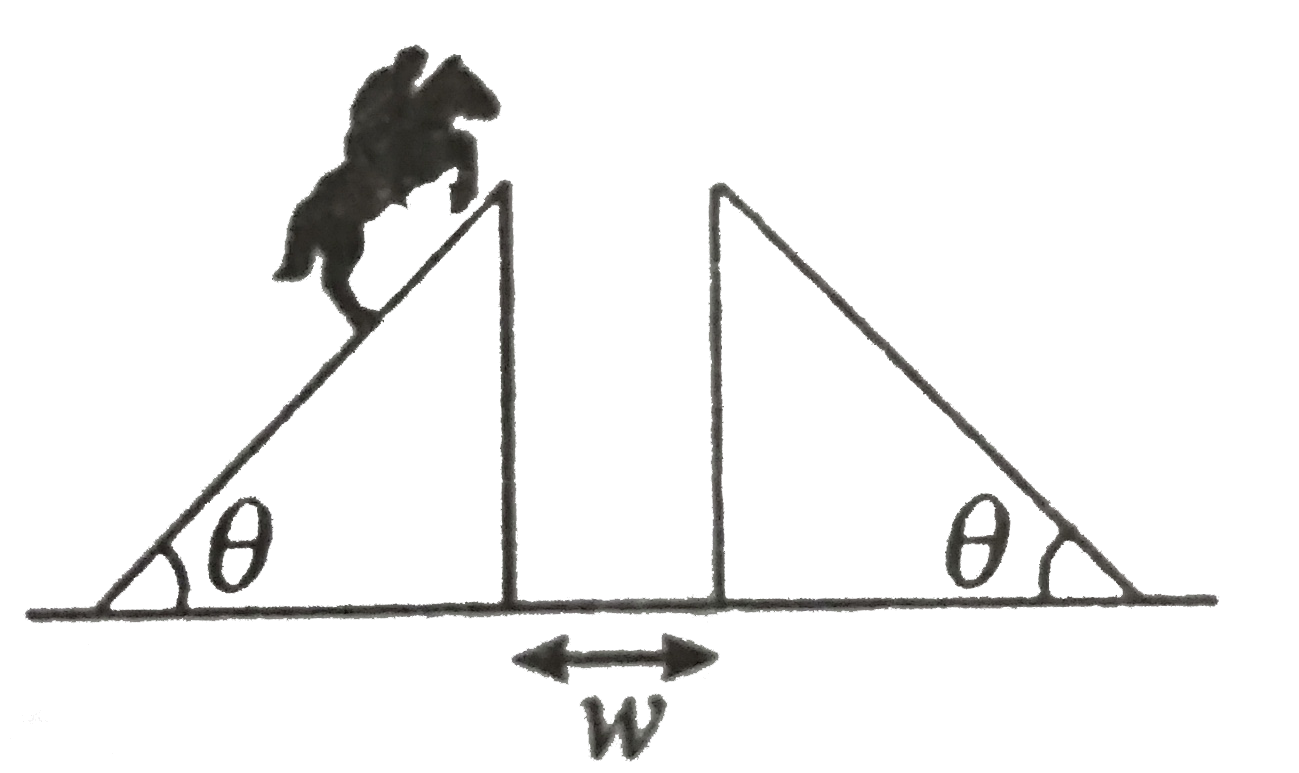
View SolutionA man is riding on a horse. He is trying to jump the gap between two symmetrical ramps of snow separated by a distance W as shown in figure. He launches off the first ramp with a speed vL. The man and the horse have a total mass m. and their size is small as compared to W. The value of initial launch speed VL which will put the horse exactly at the peak of the second ramp is
View SolutionWhen is the higher rate of energy being delivered to a light bulb higher : just after it is turned on, the glow of the filament is increasing, or after it has been on for a few seconds and the glow is steady ?

View SolutionJason ran a race of 1600 meters in two laps of equal distance. His average speeds for the first and second laps were 11 meters per second and 7 meters per second, respectively. What was his average speed for the entire race, in meters per second?
View SolutionTwo cars start together in the same direction from the same place. The first goes with uniform speed of 10km/h. The second goes at a speed of 8km/h in the first hour and increases the speed by 1/2km each succeeding hour. After how many hours will the second car overtake the first car if both cars to non-stop?
View SolutionA man is standing on top of a building 100 m high. He throws two ball vertically, one at t=0 and after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. At t=2, both the balls reach to their maximum heights at this time the vertical gap between first and second ball is +15m.
Q. The speed of first ball is
View Solution

