A ball is dropped vertically from a height d above the ground. It hits the ground and bounces up vertically to a height d/2. Neglecting subsequent motion and air resistance, its velocity v varies with the heiht h above the ground as
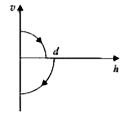
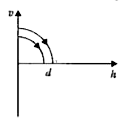
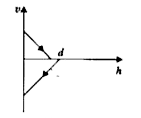

The correct Answer is:a
To solve the problem, we need to analyze the motion of the ball as it falls and bounces back up. We will derive the relationship between the velocity v of the ball and its height h above the ground.
1. Identify Initial Conditions:
- The ball is dropped from a height D (initial height).
- At the height D, the initial velocity v0=0.
2. Determine Velocity Just Before Hitting the Ground:
- As the ball falls, it accelerates due to gravity. We can use the kinematic equation:
v2=u2+2as
- Here, u=0 (initial velocity), a=g (acceleration due to gravity), and s=D (distance fallen).
- Thus, the velocity just before hitting the ground (let's call it v1) is:
v21=0+2gD⟹v1=√2gD
3. Determine Velocity After Bouncing:
- After hitting the ground, the ball bounces back to a height of D/2.
- At the maximum height of D/2, the velocity v2=0.
- We can again use the kinematic equation to find the velocity just after the bounce (let's call it v2):
v2=u2+2as
- Here, u=v1 (velocity just before hitting the ground), a=−g (deceleration going up), and s=D/2 (height reached after bouncing).
- Thus:
0=v22−2g(D2)⟹v22=gD
4. Establish Relationship Between Velocity and Height:
- From the above equations, we have:
- v21=2gD
- v22=gD
- We can express the velocity v in terms of height h:
v2=2gh(for height h falling down)
- This means that the velocity squared is proportional to the height above the ground.
5. Graphical Representation:
- The relationship v2∝h indicates that if we plot v2 against h, we will get a straight line.
- As the ball falls from height D to the ground, v will be negative, and as it bounces back to height D/2, v will be positive.
Final Conclusion:
The velocity v varies with height h above the ground according to the equation v2=2gh. This indicates a parabolic relationship when plotted.
- The ball is dropped from a height D (initial height).
- At the height D, the initial velocity v0=0.
- As the ball falls, it accelerates due to gravity. We can use the kinematic equation:
v2=u2+2as
- Here, u=0 (initial velocity), a=g (acceleration due to gravity), and s=D (distance fallen).
- Thus, the velocity just before hitting the ground (let's call it v1) is:
v21=0+2gD⟹v1=√2gD
- After hitting the ground, the ball bounces back to a height of D/2.
- At the maximum height of D/2, the velocity v2=0.
- We can again use the kinematic equation to find the velocity just after the bounce (let's call it v2):
v2=u2+2as
- Here, u=v1 (velocity just before hitting the ground), a=−g (deceleration going up), and s=D/2 (height reached after bouncing).
- Thus:
0=v22−2g(D2)⟹v22=gD
- From the above equations, we have:
- v21=2gD
- v22=gD
- We can express the velocity v in terms of height h:
v2=2gh(for height h falling down)
- This means that the velocity squared is proportional to the height above the ground.
- The relationship v2∝h indicates that if we plot v2 against h, we will get a straight line.
- As the ball falls from height D to the ground, v will be negative, and as it bounces back to height D/2, v will be positive.
The velocity v varies with height h above the ground according to the equation v2=2gh. This indicates a parabolic relationship when plotted.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics (PROJECTILE MOTION)
Explore 31 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:Dynamics ( Laws of motion )
Explore 36 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:VECTORS AND SCALARS [Selected from Previoius Years Engg. & Med. & IIT Exam Qns]
Explore 35 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
Knowledge Check
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2n
A ball is dropped from a height of 19.6 m above the ground. It rebounds from the ground and raises itself up to the same height. Take the starting point as the origin and vertically downward as the positive X-axis. Draw approximate plots of x versus t, v versus t and a versus t. Neglect the small interval during which the ball was in contact with the ground.
View SolutionA ball dropped from a height of 2 m rebounds to a height of 1.5 m after hitting the ground. Then fraction of energy lost is
View SolutionAn object is dropped from a height h from the ground. Every time it hits the ground it looses 50% of its kinetic energy. The total distance covered as t→∞ is -
View SolutionA particle (A) is dropped from a height and another particle (B) is thrown in horizontal direction with speed of 5 m/s from the same height. The correct statement is
View SolutionA body is thrown vertically upward from a point A 125 m above the ground. It goes up to a maximum height of 250 m above the ground and passes through A on its downward journey. The velocity of the body when it is at a height of 70 m above the ground is (g=10m/s2)
View SolutionA stone A is dropped from rest from a height h above the ground.A second stone B is simultaneously thrown vertically up from a point on the ground with velocity v.The line of motion of both the stones is same .Find if the value of v which would enable the stone B to meet the stone A midway between their initial positions =

View SolutionA stone is dropped from a rising balloon at a height of 76 m above the ground and reaches the ground in 6s. What was the velocity of the balloon when the stone was dropped?
View Solution