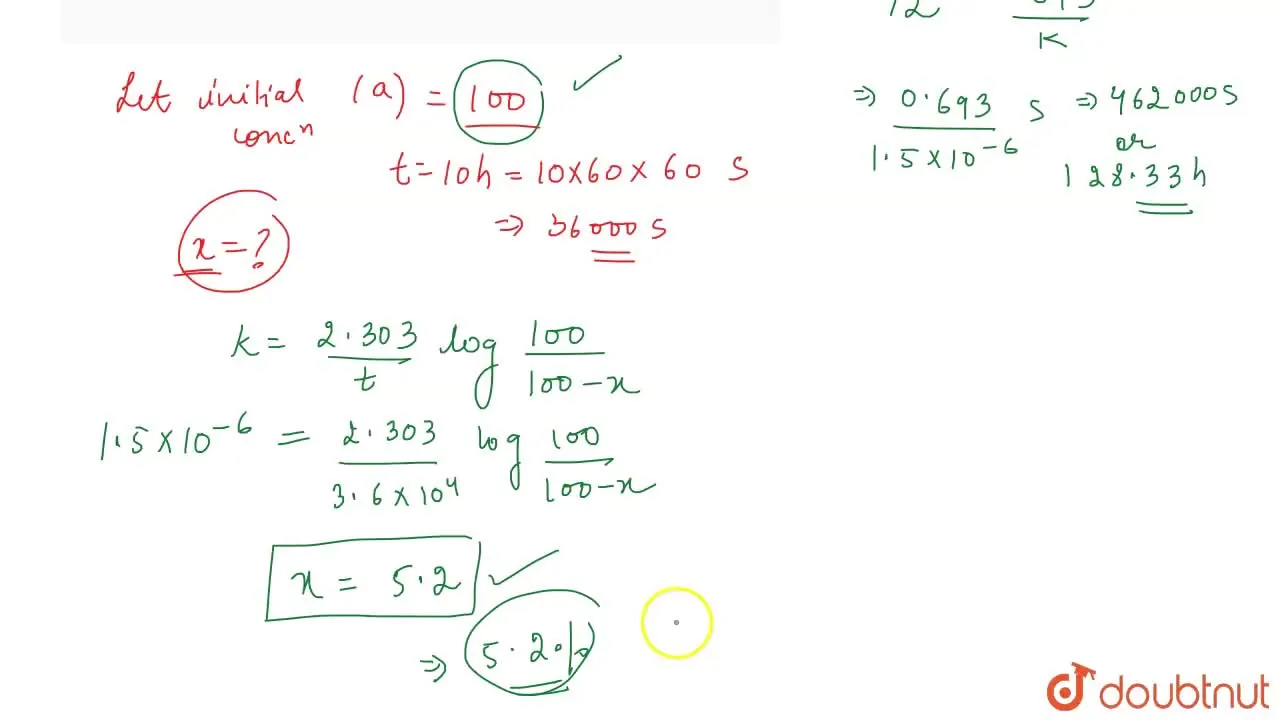The first order reaction has k=1.5×10−6 per second at 200∘C . If the reaction is allowed to ruf for 10 hours at the same temperature, what percentage of the initial concentration would have changed into the product? What is the half life period of this reaction ?
(i) Give, =1.5×10−6s−1
∴t1/2=0.693k=0.6931.5×10−6=462000s=128.33h
(ii) Let initial conc (a) = 100, t = 10h = 36000 s, x = (?)
k=2.303tlog100(100−x)
∴1.5×10−6=2.3033.6×104log100(100−x)
∴x=5.2
Thus, initial concentration changed into product is 5.2 %
Similar Questions
A first order gas reaction has k=1.5×10−6s−1 at 200∘C. If the reaction is allowed to run for 10h, what have changed in the Product? What is the half-life of this reaction?
View SolutionIn a first order reaction, the concentration of the reactants is reduced to 25% in one hour. The half-life periof of the reactions is
View Solution70% of a first order reaction was completed in 70min. What is the half life of the reaction?
View Solution90% of a first order reaction was completed in 100min.What is the half life of the reaction ?
View Solution80% of a first order reaction was completed in 70 min. What is the half life of the reaction?
View SolutionIn a first order reaction, The concentration of reactant is reduced to 1/8th of the initial concentration in 75 minutea at 298 K. What is the half period of the reaction in minutes?
View SolutionThe half life for a given reaction was doubled as the initial concentration of a reactant was doubled. What is the order of reaction.
View SolutionThe rate constant of a first order reaction is 3×10−6 per second. If the initial concentration is 0.10M, the initial rate of reaction is
View SolutionThe rate constant for a first order reaction is 5.0×10−4s−1.If initial concentration of reactant is 0.080 M, what is the half life of reaction?
View SolutionThe half-life of a chemical reaction does not change by either increasing or decreasing the initial concentration of reactant. What is the order of the reaction?
View Solution