Find the velocity of a particle moving on a line at t = 3 seconds , if its position s is in m when
s = sin (t/9)
To find the velocity of a particle moving along a line at t=3 seconds, given that its position s is defined by the equation:
s=sin(t9)
we will follow these steps:
Step 1: Understand the definition of velocity
Velocity v is defined as the rate of change of displacement with respect to time, mathematically expressed as:
v=dsdt
Step 2: Differentiate the position function
To find the velocity, we need to differentiate the position function s with respect to time t:
v=dsdt=ddt(sin(t9))
Step 3: Apply the chain rule
Using the chain rule for differentiation, we can express this as:
v=cos(t9)⋅ddt(t9)
Step 4: Differentiate t9
The derivative of t9 with respect to t is:
ddt(t9)=19
Step 5: Substitute back into the velocity equation
Now substituting this back into the velocity equation gives us:
v=cos(t9)⋅19
Step 6: Evaluate the velocity at t=3 seconds
Now we can find the velocity at t=3 seconds:
v=cos(39)⋅19=cos(13)⋅19
Final Result
Thus, the velocity of the particle at t=3 seconds is:
v=cos(13)9 m/s
---
Velocity v is defined as the rate of change of displacement with respect to time, mathematically expressed as:
To find the velocity, we need to differentiate the position function s with respect to time t:
Using the chain rule for differentiation, we can express this as:
The derivative of t9 with respect to t is:
Now substituting this back into the velocity equation gives us:
Now we can find the velocity at t=3 seconds:
Thus, the velocity of the particle at t=3 seconds is:
Topper's Solved these Questions
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:FROM SCALAR PRODUCT AND VECTOR PRODUCT
Explore 20 Videos
- UNITSBook:ICSEChapter:UNITSExercise:MODULE 3 (SELECTED PROBLEMS)
Explore 38 Videos
- WAVESBook:ICSEChapter:WAVESExercise:From Musical Sound
Explore 10 Videos
Similar Questions
Find the velocity of a particle moving on a line at t = 3 seconds , if its position s is in m when
s = log t and
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?
View SolutionFigure shows the velocity time graph of a particle moving along straight line (v is m/s and t is in second). It average velocity in 20 seconds will be:
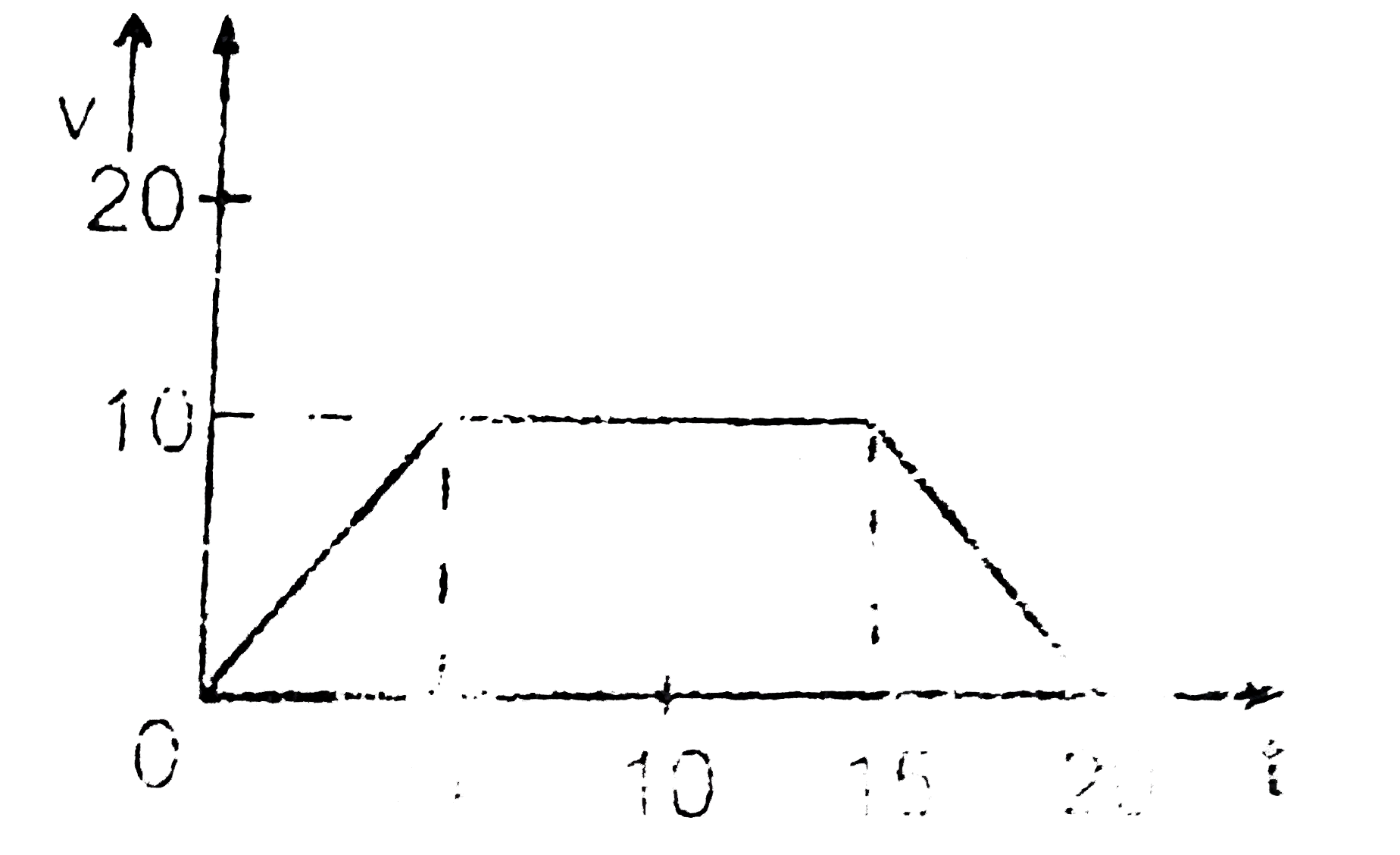 .
.
View SolutionThe velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
View Solutionx-coordinate of a particle moving along this axis is x=(2+t2+2t3). Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at t=2s.
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?
View Solution

