In ΔPQR, MN is parallel to QR and PMMQ=23
(i) Find MNQR
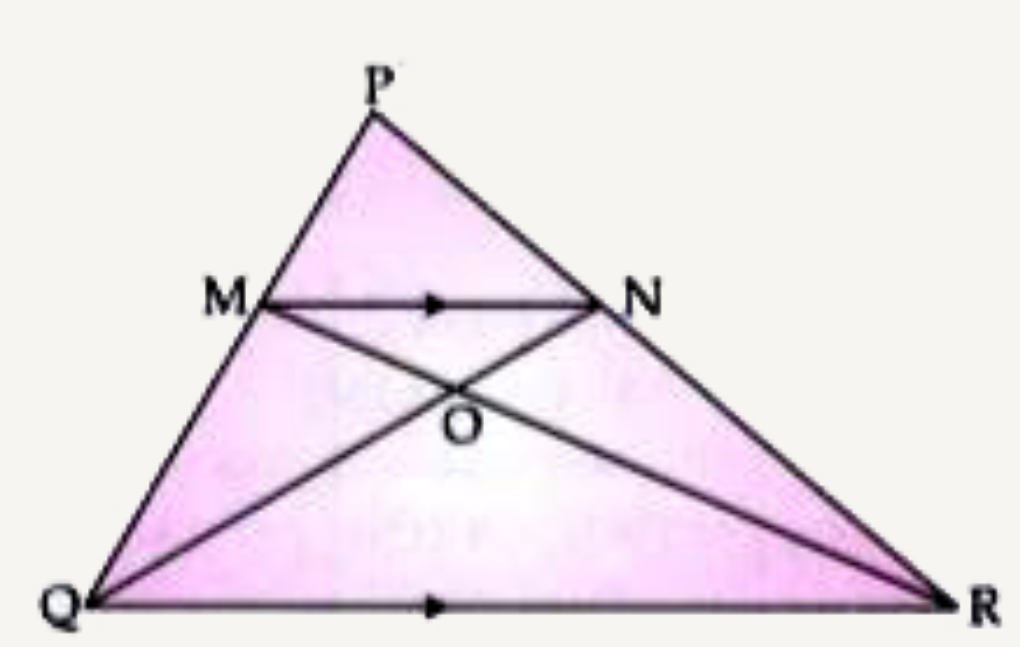
The correct Answer is:25
Step by step video & image solution for In DeltaPQR, MN is parallel to QR and (PM)/(MQ)=2/(3) (i) Find (MN)/(QR) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
In ΔPQR, MN is parallel to QR and PMMQ=23
(iii) Find, Area of ΔOMN : Area of ΔORQ.
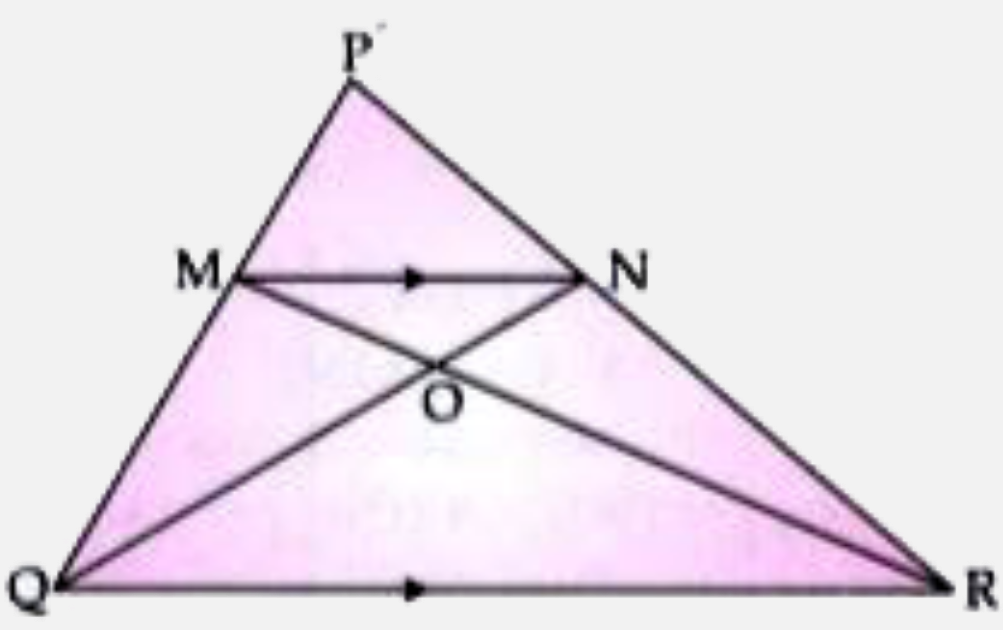 View Solution
View SolutionIn ΔPQR, MN is parallel to QR and PMMQ=23
Prove that ΔOMNandΔORQ are similar.
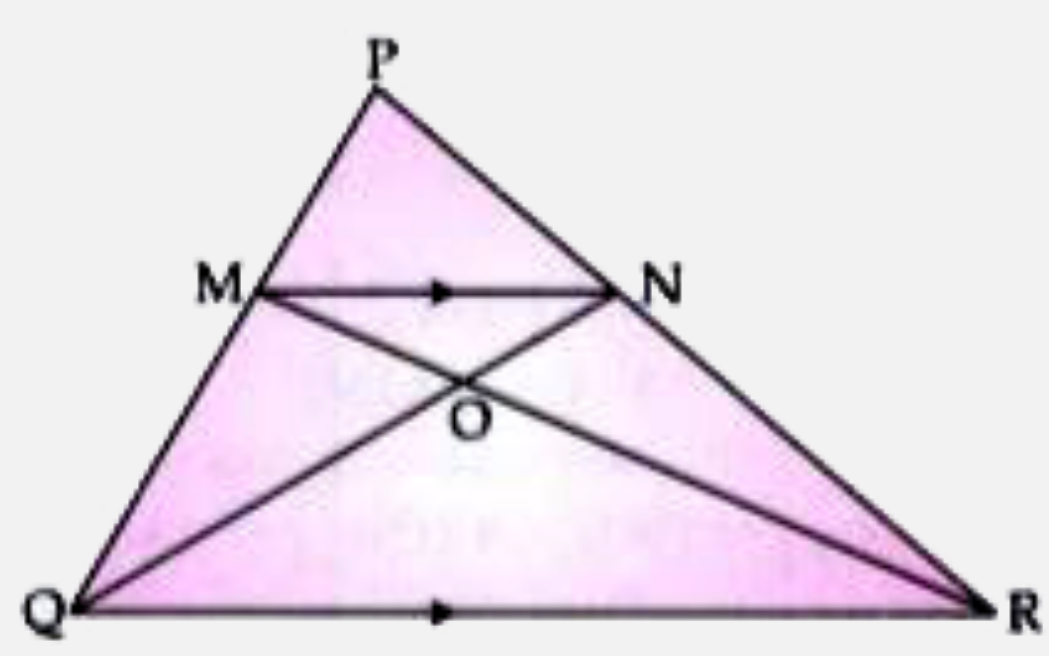 View Solution
View SolutionIn the figure PQ is parallel to MN if KPPM=413andKN=20.4.
Find KQ.
 View Solution
View SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.
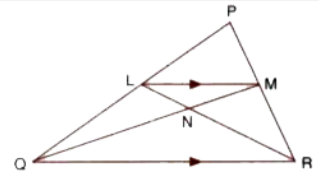
Calculate the value of ratio :
PLPQ and then LMQRView SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.

Calculate the value of ratio :
Area of ΔLMNArea of ΔMNRView SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.

Calculate the value of ratio :
Area of ΔLQMArea ofΔLQNView SolutionIn ΔPQR,∠Q=90∘ and QM is perpendicular to PR. Prove that :
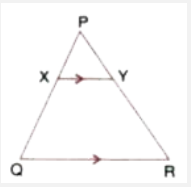
PQ2+QR2=PR2View SolutionThe given figure shows P a triangle PQR in which XY is parallel to QR. If PX : XQ = 1:3 and QR = 9 cm, find the length of XY. Further, if the area of ΔPXY=xcm2, find, in terms of x, the area of :
trapezium XQRY.
 View Solution
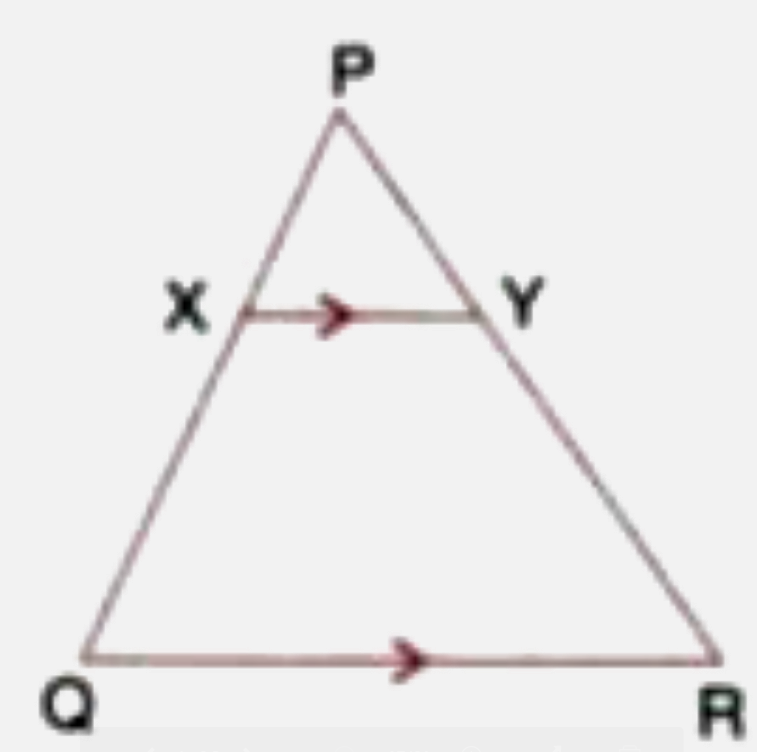
View SolutionThe given figure shows P a triangle PQR in which XY is parallel to QR. If PX : XQ = 1:3 and QR = 9 cm, find the length of XY. Further, if the area of ΔPXY=xcm2, find, in terms of x, the area of :
triangle PQR.
 View Solution
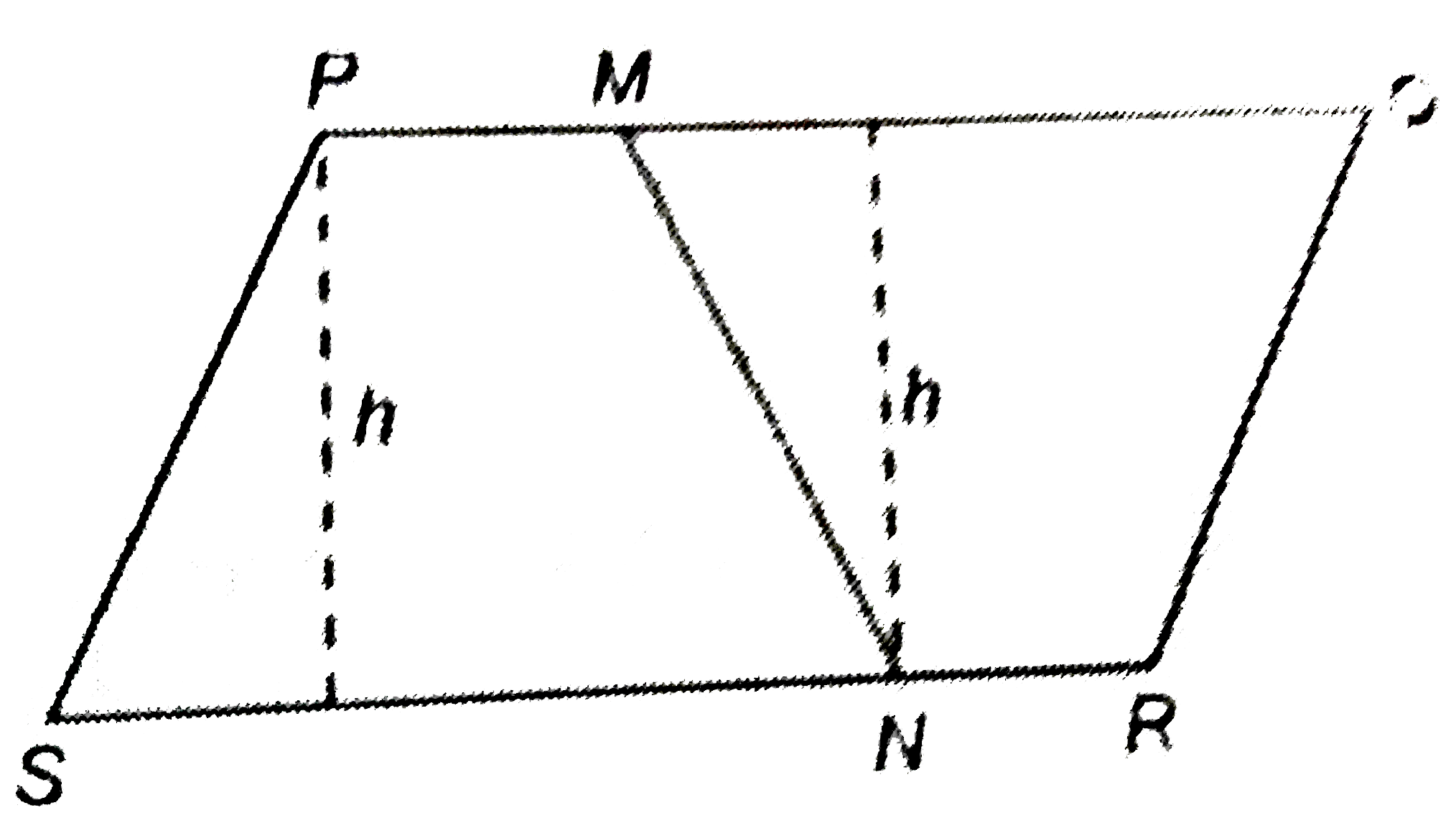
View SolutionPQRS is a parallclogram such that PQ is parallel to SR and SP is parallel to RQ. The length of side PQ is 20 cm. M is point between P and Q such that the length of PM is 3 cm. N is a points between points S and R. Find the length of SN such that segmen MN divides the paralelogram in two regions with equal areas.
 View Solution
View Solution
