In the figure PQ is parallel to MN if KPPM=413andKN=20.4.
Find KQ.

Given In DeltaKMN,PQ||MN
KPPM=KQQN ( by B.P.T or Thale's theorem)
Let KQ=x, then QN= 20.4 -x
now from (1)
413=x20.4−x
81.6−4x=13x
17x=81.6
x= 4.8 cm
Therefore KQ= 4.8 cm
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In Figure PQ is parallel to MN. if KPPM=4/13 and KN=20.4cm. Find KQ.
View SolutionIn ΔPQR, MN is parallel to QR and PMMQ=23
(i) Find MNQR
View SolutionIn the given figure, QR is parallel to AB and DR is parallel to QB.
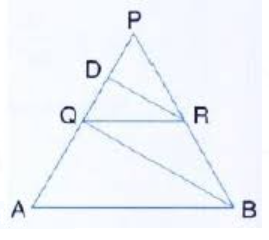
Prove that : PQ2=PD×PA.
View SolutionWhere line XY is parallel to line QU.
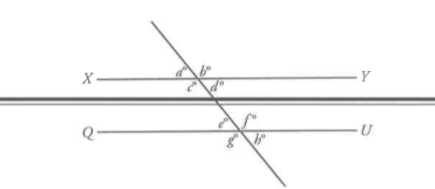
If g=11y,a=4x−yandd=5y+2x−20. Find h.
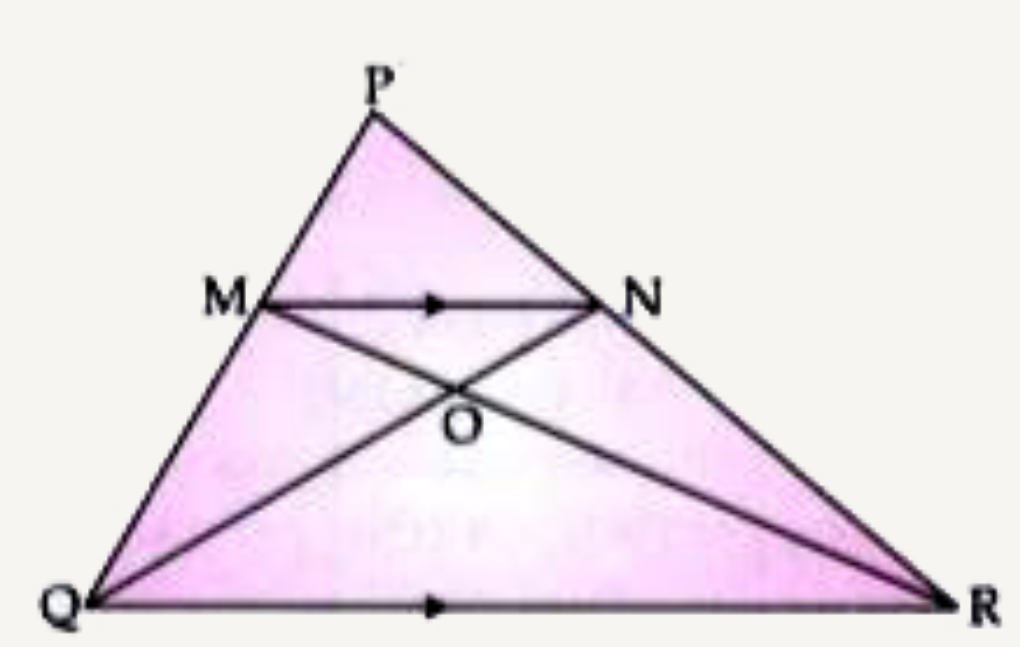
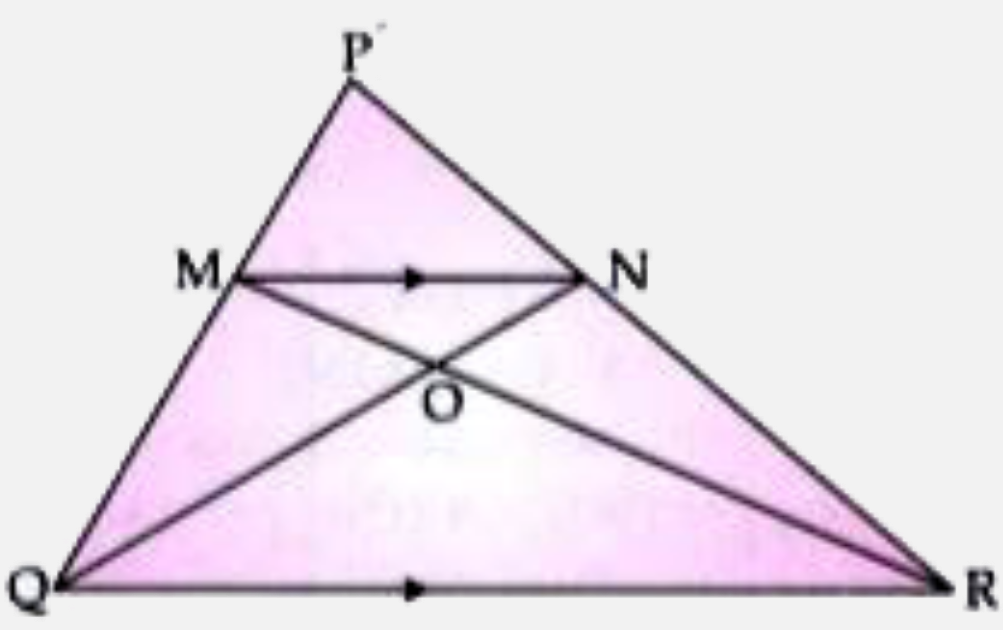
View SolutionIn ΔPQR, MN is parallel to QR and PMMQ=23
(iii) Find, Area of ΔOMN : Area of ΔORQ.
View SolutionIn the given triangle PQR, LM is parallel to QR and PM : MR = 3: 4.
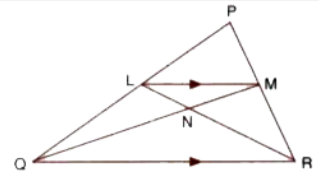
Calculate the value of ratio :
PLPQ and then LMQR
View SolutionIn the given figure, PQ//AB, CQ = 4.8 cm QB = 3.6 cm and AB = 6-3 cm. Find :

PQ
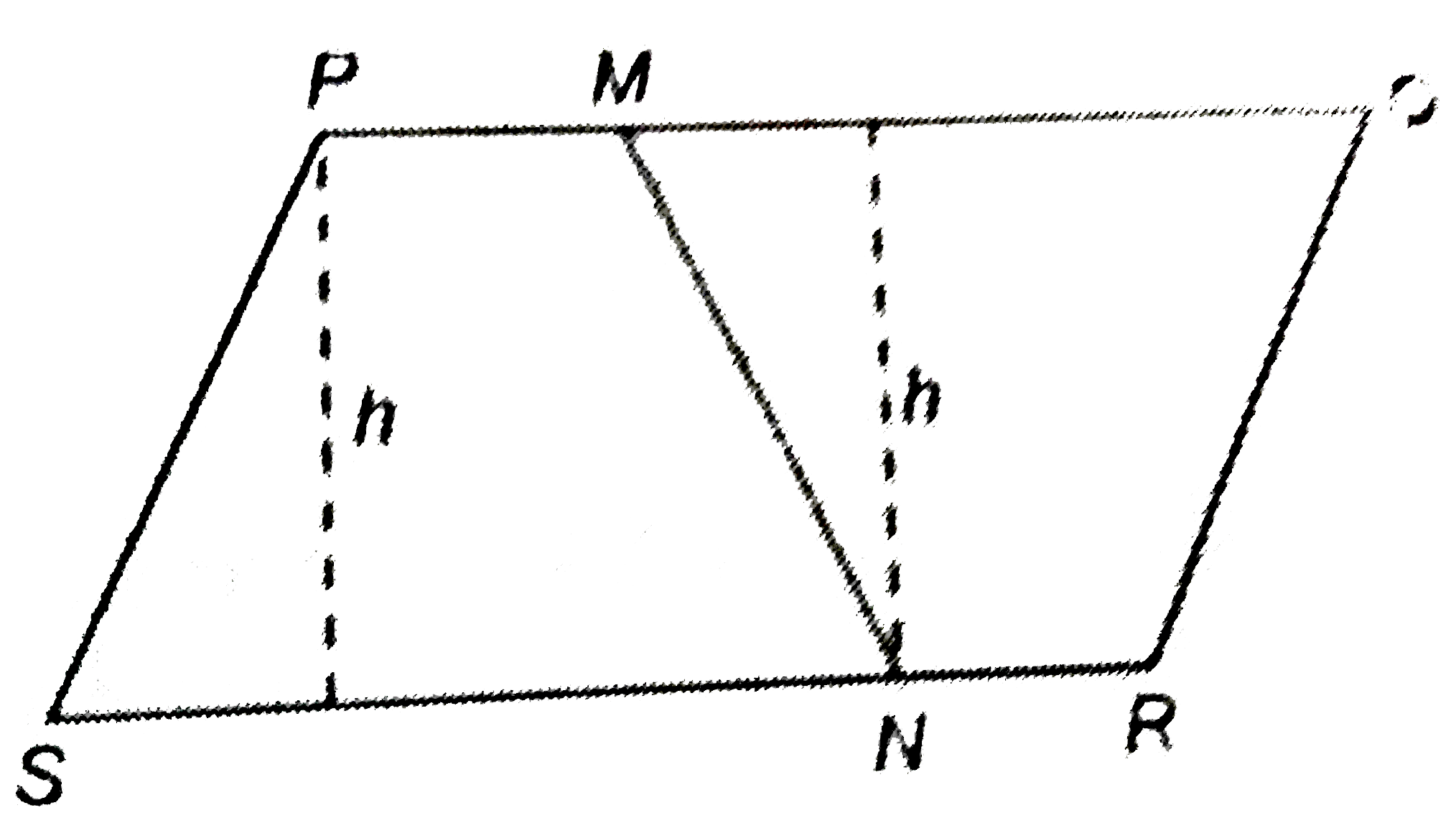
View SolutionPQRS is a parallclogram such that PQ is parallel to SR and SP is parallel to RQ. The length of side PQ is 20 cm. M is point between P and Q such that the length of PM is 3 cm. N is a points between points S and R. Find the length of SN such that segmen MN divides the paralelogram in two regions with equal areas.
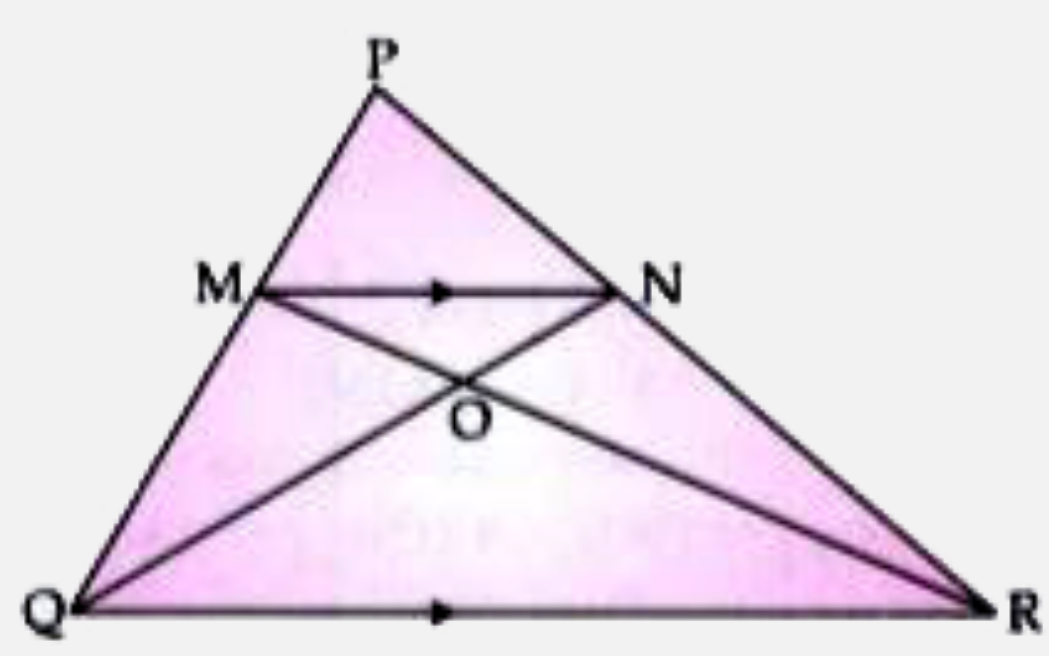
View SolutionIn ΔPQR, MN is parallel to QR and PMMQ=23
Prove that ΔOMNandΔORQ are similar.
View SolutionIn the given figure if PQ||YZ. Find XQ.

View Solution
