Find the number of triangles whose angular points are at the angular points of a given polygon of n sides, but none of whose sides are the sides of the polygon.
Video Solution
Text Solution
A polygon of n sides has n angular points. Number of triangles formed from these n angular points=.nC3.
These are comprised of two exclusive cases viz.
(i) atleast one side of the triangle is a side of the polygon.
(ii) no side of the triangle is a side of the polygon.
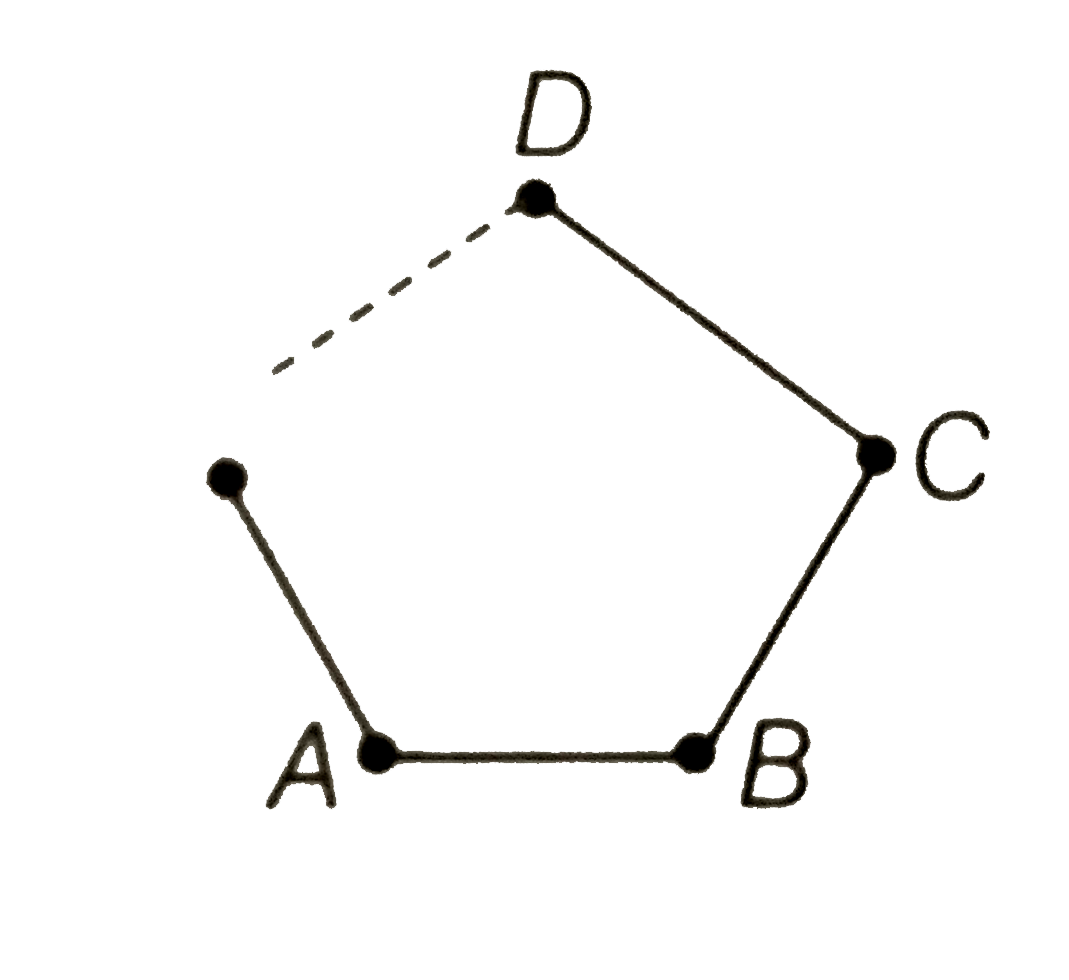
Let AB be one side of the polygon. if each angular point of the remaining (n-2) points are joined with A and B, we get a triangle with one side AB.
∴Number of triangles of which AB is one side=(n-2)
Likewise, number of triangles of which BC is one side=(n-2) and of which atleast one side is the side of the polygon=n(n-2).
Out of these triangle, some are counted twice. for example, the triangle when C is joined with AB is ΔABC, is taken when AB is taken as one side. again triangle formed when A is joined with BC is counted when BC is taken as one side.
So, the number of triangles of which one side is the side of the triangle.
=n(n−2)−n=n(n−3)
=.nC3−n(n−3)=16n(n−4)(n−5)
|
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - JEE Type Solved Examples: Single Matching Type Questions
1 Video
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise For Session 1
11 Videos
- PARABOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
36 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
Similar Questions
Knowledge Check
The number of diagonals of a polygon of 20 of sides
A210B190C180D170
The number of triangles whose vertices are a the vertices of an octagon but none of whose sides happen to come from the sides of the octagon is
View SolutionThe number of diagonals of a polygon of 15 sides is:
View SolutionFind the numbers of diagonals in the polygon of n sides.
View SolutionFind the number of diagonals in the convex polygon of n sides .
View SolutionFind the number of diagonals of a 16-sided polygon.
View SolutionA regular polygon of 10 sides is constructed. Triangles are formed joining vertices of the polygon. Find the number of triangles
(i) if two sides of trinangle coincide with the sides of polygon.
(ii) if only one side of triangle coincide with the side of polygon.
View SolutionIn a polygon the number of diagonals 77. Find the number of sides of the polygon.
View Solution
