Consider all possible permutations of the letters of the word ENDEANOEL. Match the statements/ expressions in column I with the statement/expressions in

The correct Answer is:A, B, C, D
(A)→(p),(B)→(s),(C)→(q),(D)→(q)
(A) ENDEA, N,O,E,L are five different letters, then perrmutations=5!.
(B) if E is in the first and last position, then permutations
=7!2!=7×6×5!2=21×5!
(C) for first four letters=4!2!=4×3=12 and for last five
letters=5!3!=5!6, then permutations =12×4!2!=12, then permutations =5!3!×12=5!6×12=2×5!
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Subjective Type Questions)
16 Videos
- PARABOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
36 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
Similar Questions
Match the statements in column A with those in column B

View SolutionConsider all possible permutations of the letters of the word ENDEANOEL. The number of permutations containing the word ENDEA is
View SolutionMatch the conditions/ expressions in Column I with statement in Column II
View SolutionMatch the statements in column A, with those in column B

View SolutionMatch the statements in column A, with those in column B.

View SolutionConsider all possible permutations of the letters of the word ENDEANOEL. The number of permutations in which the letter E occurs in the first and last positions is
View SolutionConsider all possible permutations of the letters of the word ENDEANOEL. The number of permutations in which none of the letters D, L and N occurs in the last positions is
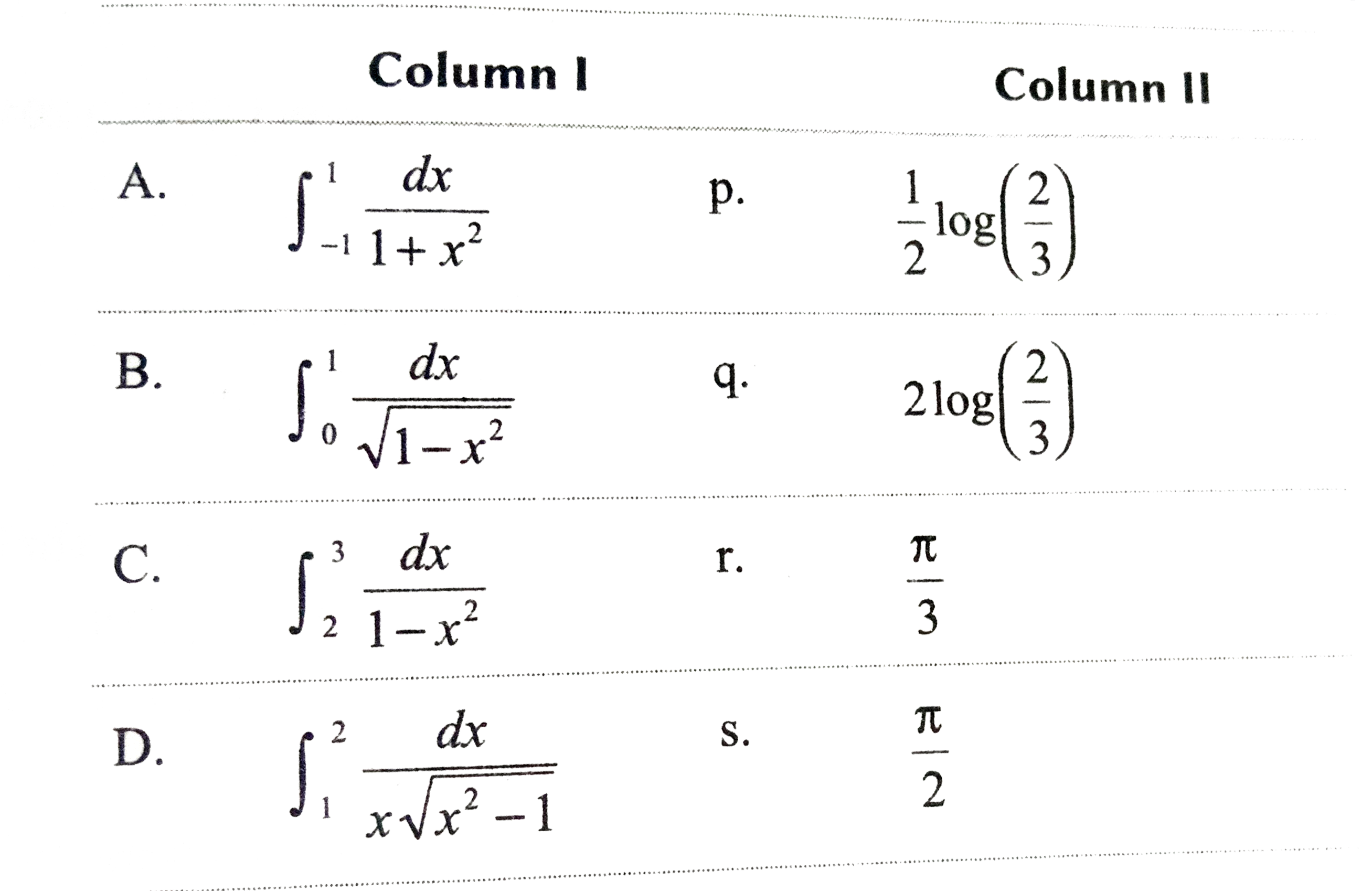
View SolutionMatch the conditions / expression in Column I with statement in Column II.
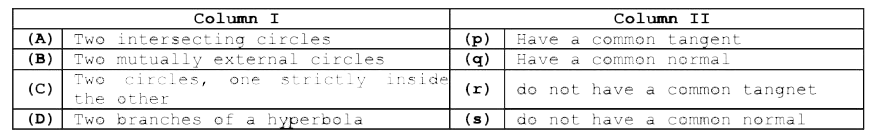
View SolutionMatch the conics in List I with the statements/expressions in List II


View SolutionMatch the entries in column II with the statements given in column I.

View Solution
