In a plane there two families of lines : y=x+r, y=-x+r, where r∈{0,1,2,3,4}. The number of the squares of the diagonal of length 2 formed by these lines is____.
9
16
32⋅.4C2
5C2+.3P2
The correct Answer is:A, C
There are two sets of five parallel lines at equal distance. Clearly, lines like l1,l3,m1andm3 form a square whose diagonal's length is 2.
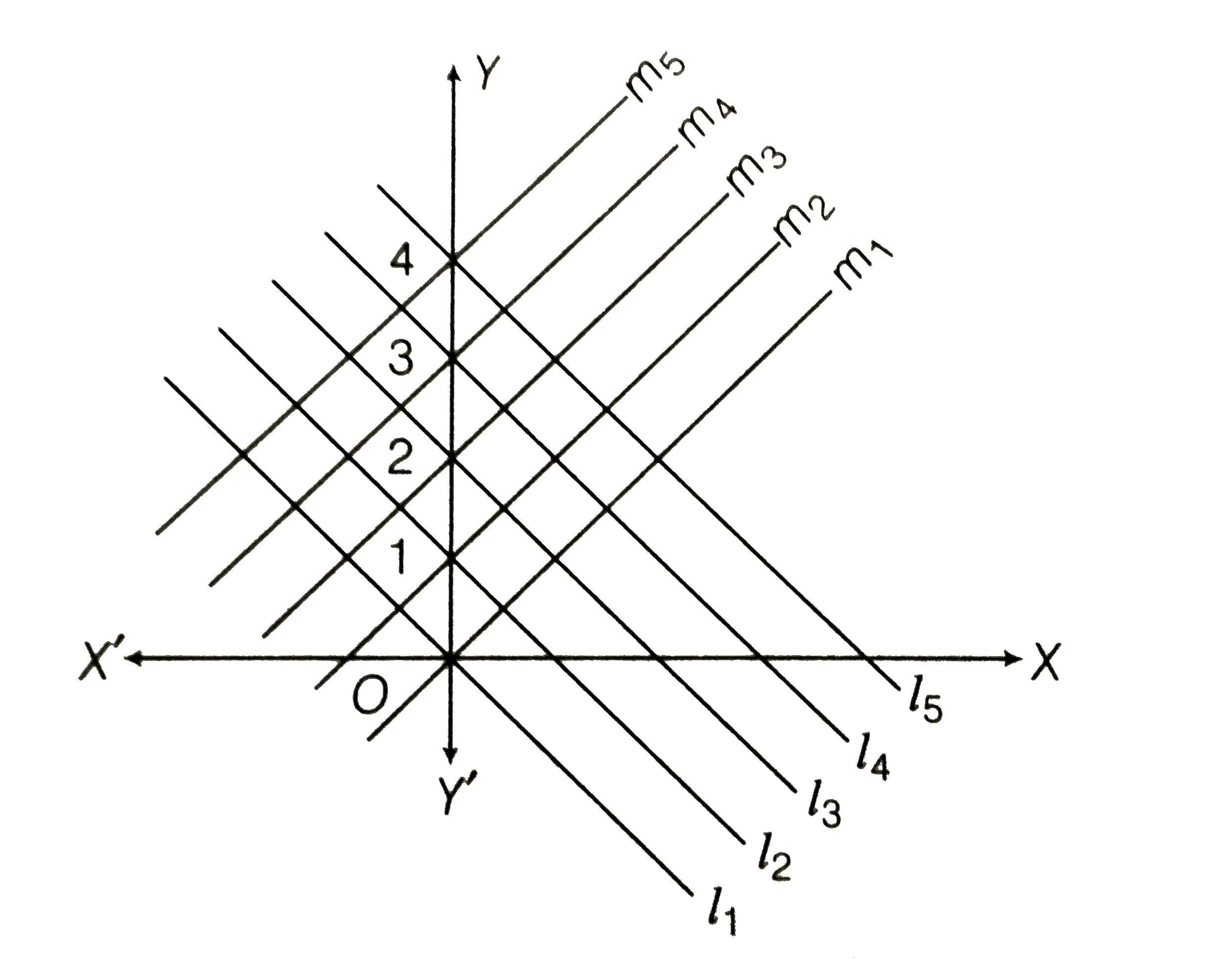
∴Number of required squares=3×3=9=32⋅.4C2
[∵ are (l1,l2),(l2,l4)and(l3,l5) for one set, etc.]
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS Book:ARIHANT MATHS ENGLISHChapter:PERMUTATIONS AND COMBINATIONS Exercise:JEE Type Solved Examples: Single Matching Type Questions
Explore 1 Video
- PERMUTATIONS AND COMBINATIONS Book:ARIHANT MATHS ENGLISHChapter:PERMUTATIONS AND COMBINATIONS Exercise:Exercise For Session 1
Explore 11 Videos
- PARABOLABook:ARIHANT MATHS ENGLISHChapter:PARABOLAExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 36 Videos
- PROBABILITYBook:ARIHANT MATHS ENGLISHChapter:PROBABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 54 Videos
Similar Questions
In a plane there are two families of lines y=x+r,y=−x+r, where r∈{0,1,2,3,4}. The number of squares of diagonals of length 2 formed by the lines is:
View SolutionIn a plane there are two families of lines y=x+r,y=−x+r, where r∈{0,1,2,3,4}. The number of squares of diagonals of length 2 formed by the lines is:
View Solution
Knowledge Check
Equations of diagonals of the square formed by the lines x=0,y=0,x=1 and y=1 are
Ay=x,x+y=2B2y=x,y+x=13Cy=x,y+x=1Dy=2x,y+2x=1
Find the equations of the diagonals of the square formed by the lines x=0,y=0,x=1 and y=1.
View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
View SolutionArea of the triangle formed by the lines y2−9xy+18x2=0andy=9 is____
View SolutionArea of the triangle formed by the lines x2+4xy+y2=0andx−y=4 is____
View SolutionThe diagonal of the rectangle formed by the lines x2−7x+6=0 and y2−14y+40=0 is
View SolutionConsider a family of lines (4a+3)x−(a+1)y−(2a+1)=0 where a∈R a member of this family with positive gradient making an angle of 45 with the line 3x−4y=2, is
View Solution