There are three stations A,B and C five routes for going from station A to station B and four routes for going from station B to station C. find number of different ways through which a person can go from A to C via B.
To solve the problem, we need to determine the number of different ways a person can travel from station A to station C via station B.
Step 1: Identify the routes from A to B.
- There are 5 different routes available for traveling from station A to station B.
Step 2: Identify the routes from B to C.
- There are 4 different routes available for traveling from station B to station C.
Step 3: Apply the Fundamental Principle of Counting.
- According to the Fundamental Principle of Counting, if there are m ways to do one thing and n ways to do another, then there are m×n ways to perform both actions.
- Here, the action of going from A to B has 5 options, and the action of going from B to C has 4 options.
Step 4: Calculate the total number of ways.
- The total number of ways to go from A to C via B is calculated as:
Total ways=(Ways from A to B)×(Ways from B to C)=5×4=20
Thus, the total number of different ways through which a person can go from A to C via B is 20.
---
- There are 5 different routes available for traveling from station A to station B.
- There are 4 different routes available for traveling from station B to station C.
- According to the Fundamental Principle of Counting, if there are m ways to do one thing and n ways to do another, then there are m×n ways to perform both actions.
- Here, the action of going from A to B has 5 options, and the action of going from B to C has 4 options.
- The total number of ways to go from A to C via B is calculated as:
Total ways=(Ways from A to B)×(Ways from B to C)=5×4=20
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS Book:ARIHANT MATHS ENGLISHChapter:PERMUTATIONS AND COMBINATIONS Exercise:JEE Type Solved Examples: Single Matching Type Questions
Explore 1 Video
- PERMUTATIONS AND COMBINATIONS Book:ARIHANT MATHS ENGLISHChapter:PERMUTATIONS AND COMBINATIONS Exercise:Exercise For Session 1
Explore 11 Videos
- PARABOLABook:ARIHANT MATHS ENGLISHChapter:PARABOLAExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 36 Videos
- PROBABILITYBook:ARIHANT MATHS ENGLISHChapter:PROBABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 54 Videos
Similar Questions
A person wants to leave station B. There are three routes from station B to A and four routes from B to c. In how many ways can he leave the station B.
View SolutionThere are 5 routes ferom A to B and 3 routes from place B to place C. Find how many different routes are there from A to C via B.
View SolutionA person wants to go from station A to station C via station b. There are three routes from A to B four routes from B to C. In how many ways can he travel from A to C?
View Solution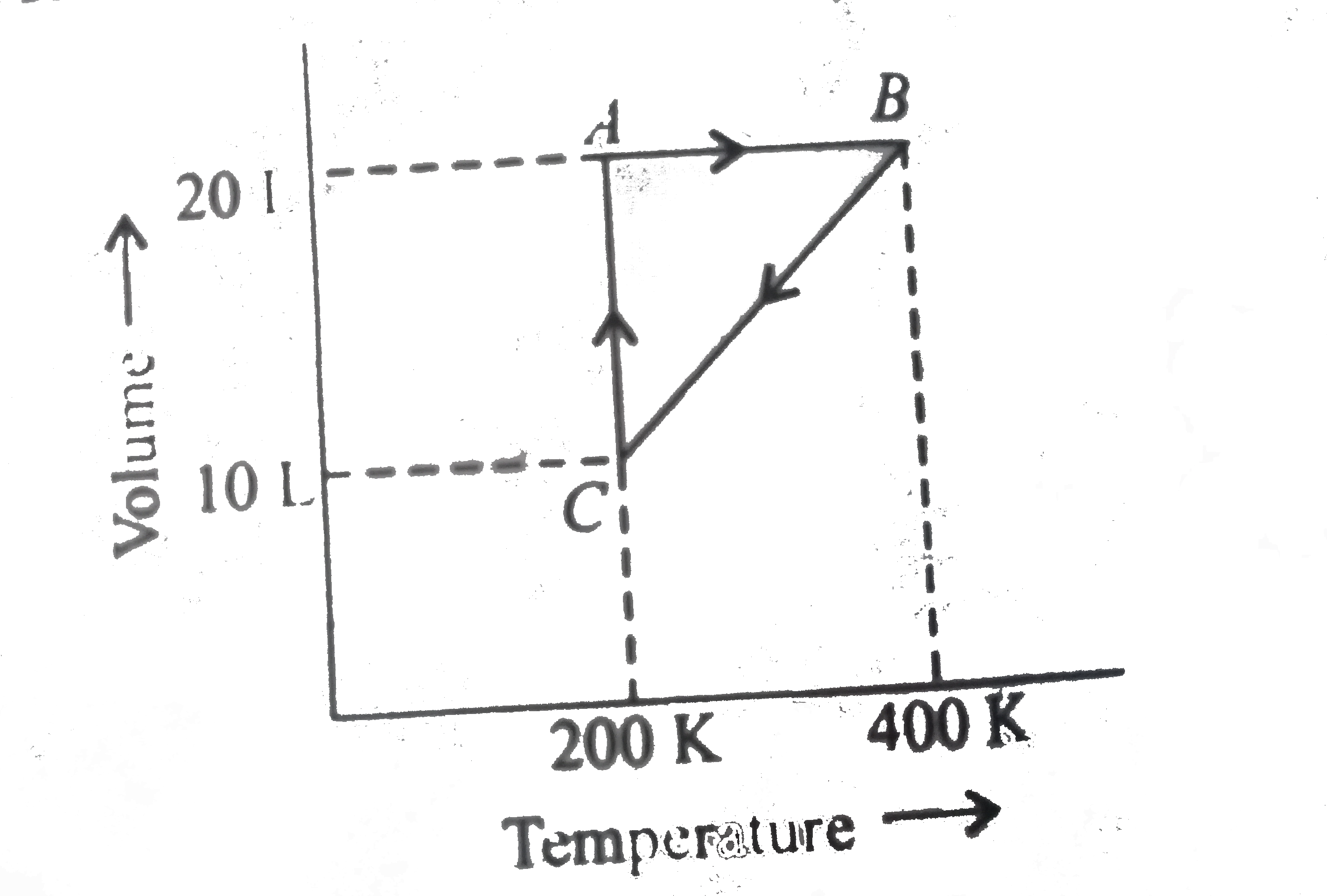
The process which occurs in going from B→C is
View SolutionThere are five routes for a journey from stations . A to B . In how many different ways can a man go from A to B and return , if for returning.
any of the routes is taken
View SolutionThere are five routes for a journey from stations . A to B . In how many different ways can a man go from A to B and return , if for returning.
the same route is taken
View SolutionThere are five routes for a journey from stations . A to B . In how many different ways can a man go from A to B and return , if for returning.
the same route is not taken?
View SolutionA train travels with a speed of 60 km h−1' from station A to station B and then comes back with a speed 80 km h−1' from station B to station A. Find : (i) the average speed, and (ii) the average velocity of train.
View SolutionA train takes 3 h to reach from station A to station B at a distance of 400 km and 5 h in its return journey. Find the average speed of the train.
View SolutionFrom Delhi station, if we buy 2 tickets for station A and 3 tickets for station B, the total cost is 77. But if we buy 3 tickets for station A and 5 tickets for station B, the total cost is 124. What are the fares from Delhi to station A and to station B?
View Solution

