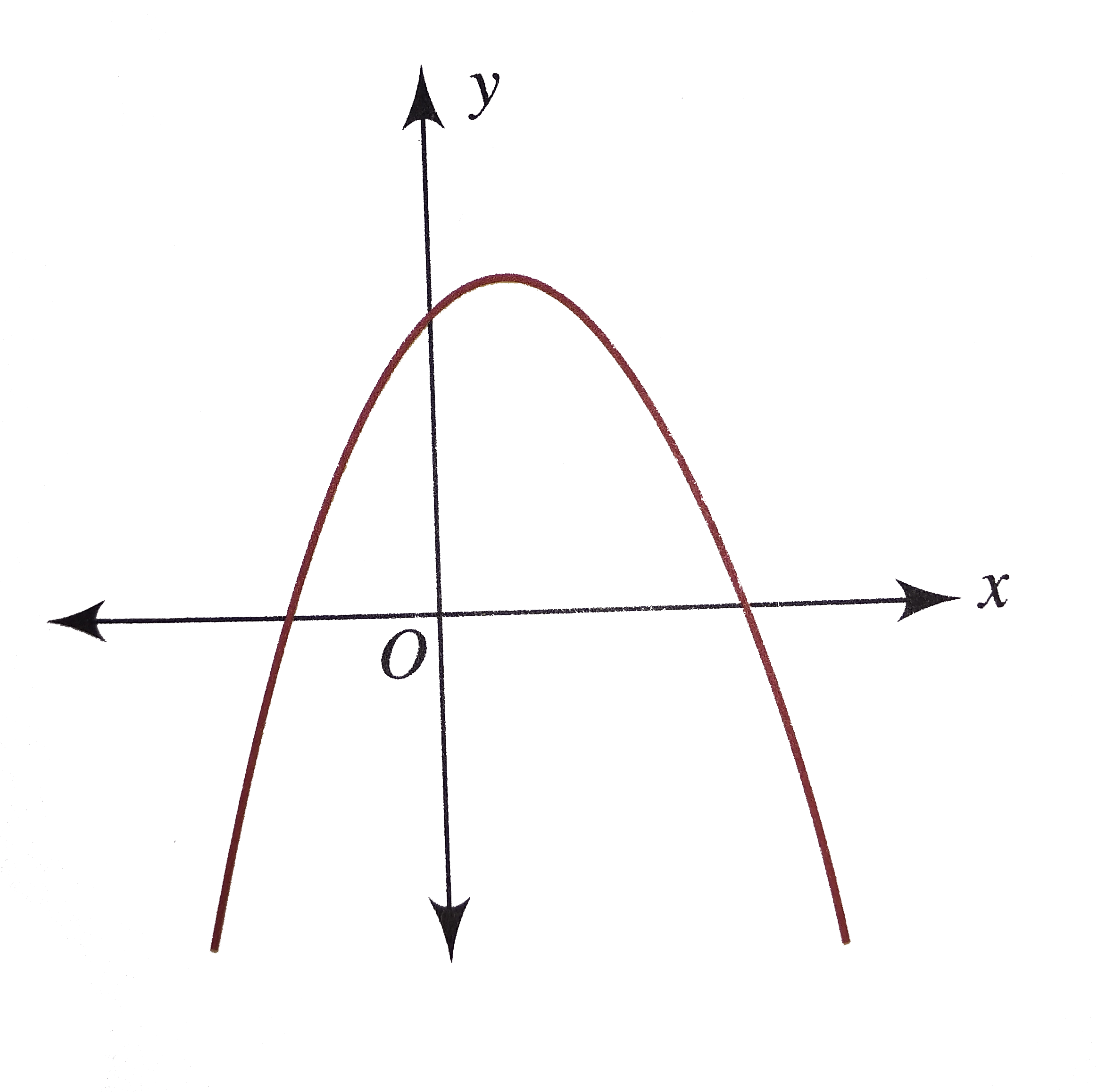
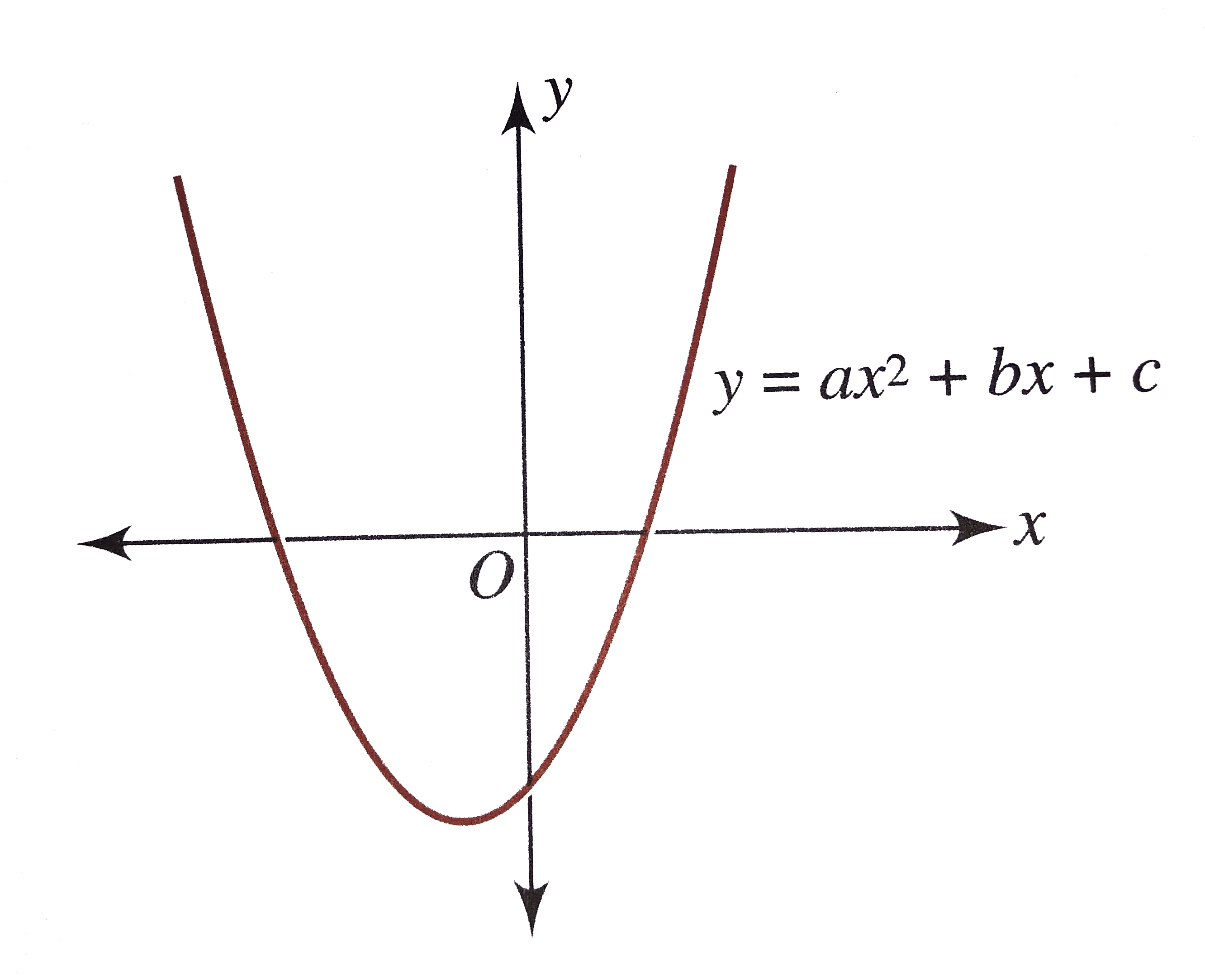The adjoining graph of y=ax2+bx+c shows that
A
(a) a<0
B
(b) b2<4ac
C
(c) c>0
D
(d) a and b are of opposite signs
Video Solution
Text Solution
The correct Answer is:A, D
It is clear from graph that the equation y=ax2+bx+c=0 has two real and distinct roots. Therefore
b2−4ac>0………..i
∴ Parabola open downwards.
a<0
and y=ax2+bx+c cuts off Y axis at x=0
∴y=c<0
⇒c<0
and x-coordinate of vertex >0
⇒−b2a>0⇒ba<0
⇒b>0[∵a<0]
It is clear that a and b are of opposite signs.
|
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Passage Based Questions)
21 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - SCQ_TYPE
1 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
17 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
Knowledge Check
The graph of y=ax2+bx+c passes through the points (1,−8),(2,−1),(3,4),and(5,8). If the maximum value of y-coordinate at x=5, through which outer other point must be graph of y pass?
A(4,6)B(6,4)C(8,−1)D(10,−8)If in the quadratic function f(x)=ax2+bx+c, a and c are both negative constant, which of the following could be the graph of function f?
A B
B C
C D
D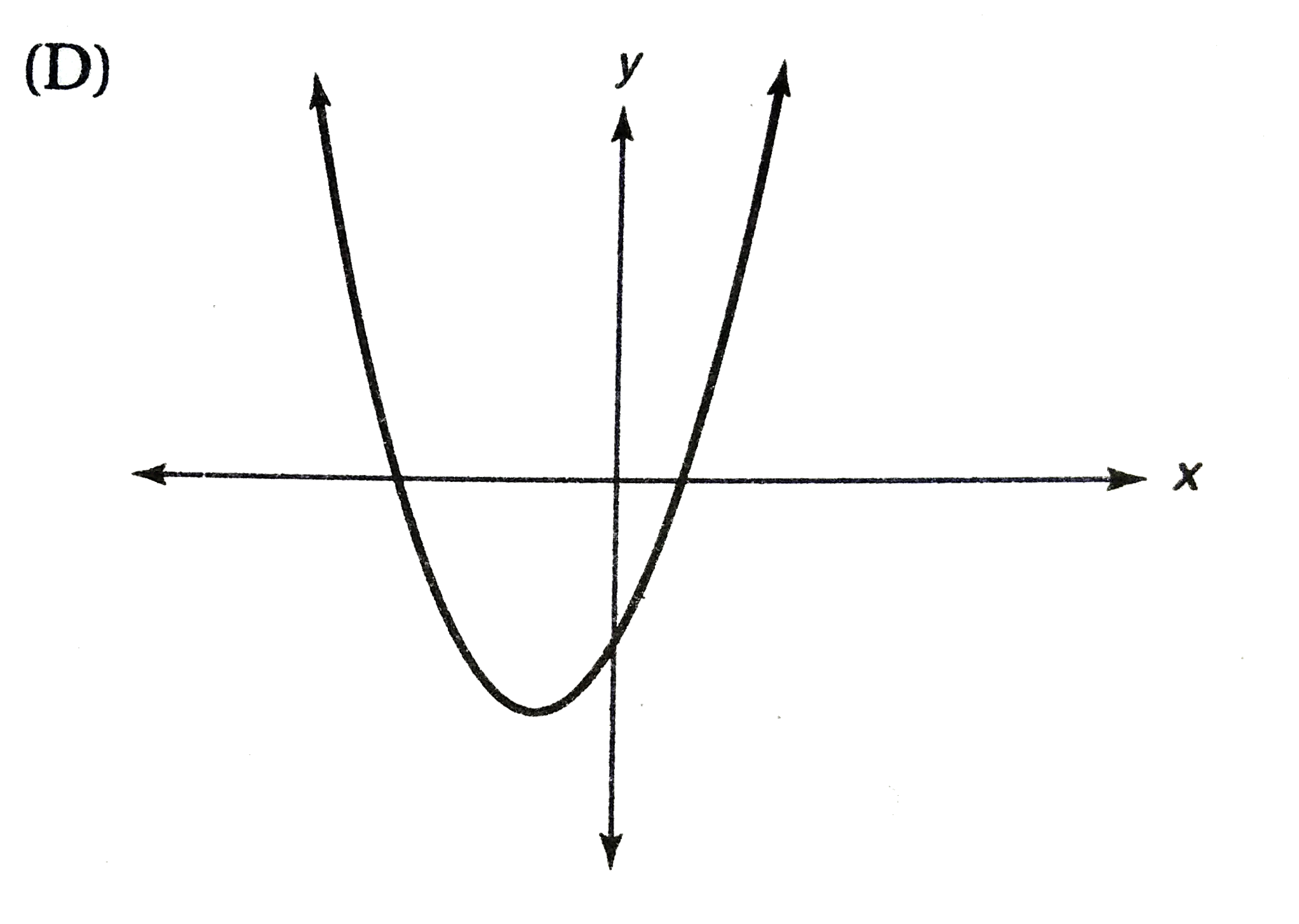
The following figure shows the graph of f(x)=ax2+bx+c, find the signs of a,bandc.
View Solution∫(ax2+bx+c)dx =
View SolutionThe vertex or the parabola y = ax2+bx+c is
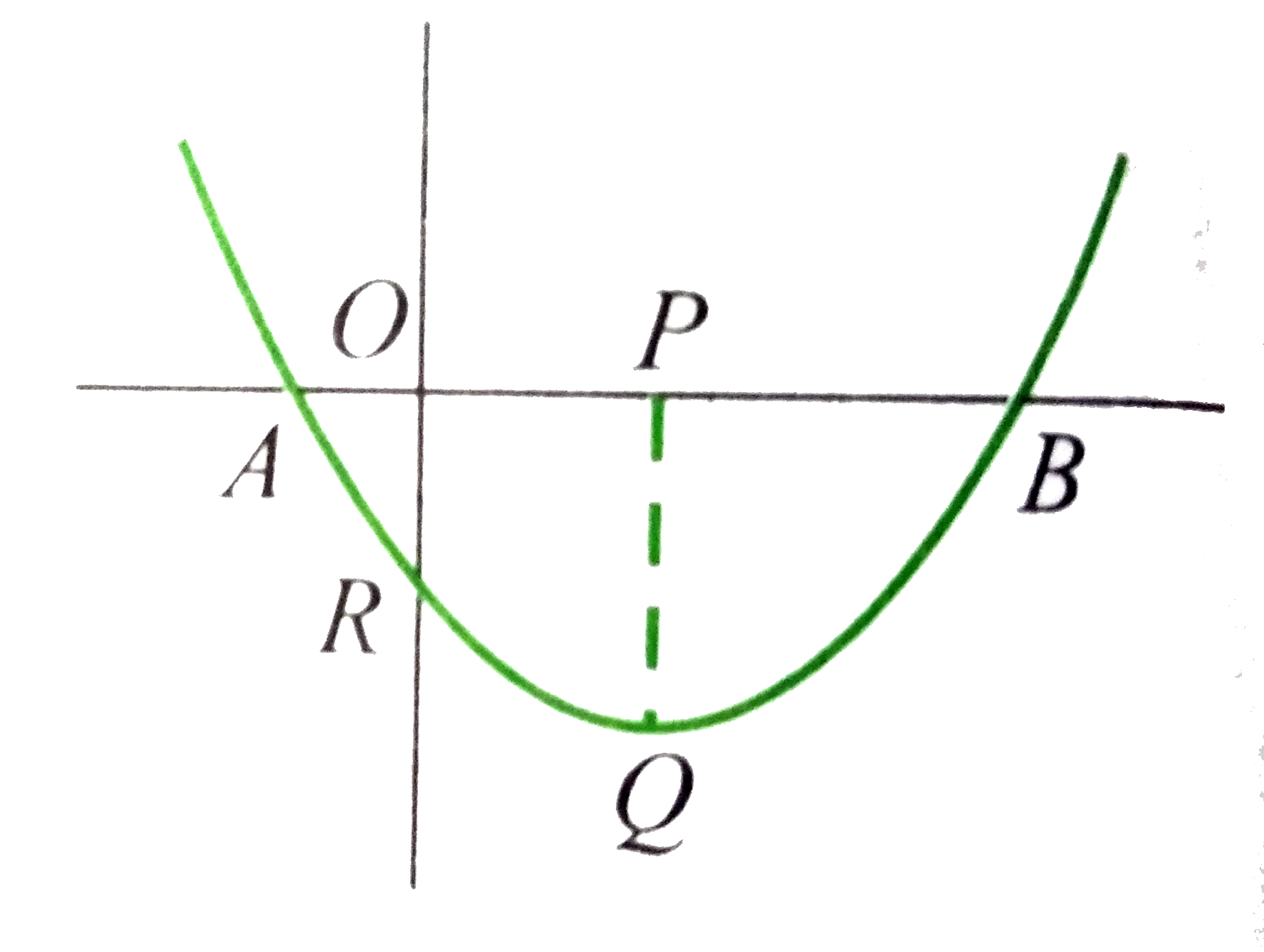
View SolutionGraph of y = ax^(2) + bx + c is as shown in the figure . If PQ=9,
OR=5 and OB=2.5, the which of the following is /are ture?
View SolutionThe tangent to y=ax2+bx+c at (1,2) is parallel to the normal at the point (−2,2) on the same curve. Find the value of 3a−b+c
View SolutionThe quadratic equation ax2+bx+c=0 has real roots if:
View Solution