ax2+bx+c=0(a>0), has two roots αandβ such α<−2andβ>2, then
4a−2|b|+c<0
9a−3|b|+c<0
a−|b|+c<0
c<0,b2−4ac>0
The correct Answer is:A, C, D
Here D>0
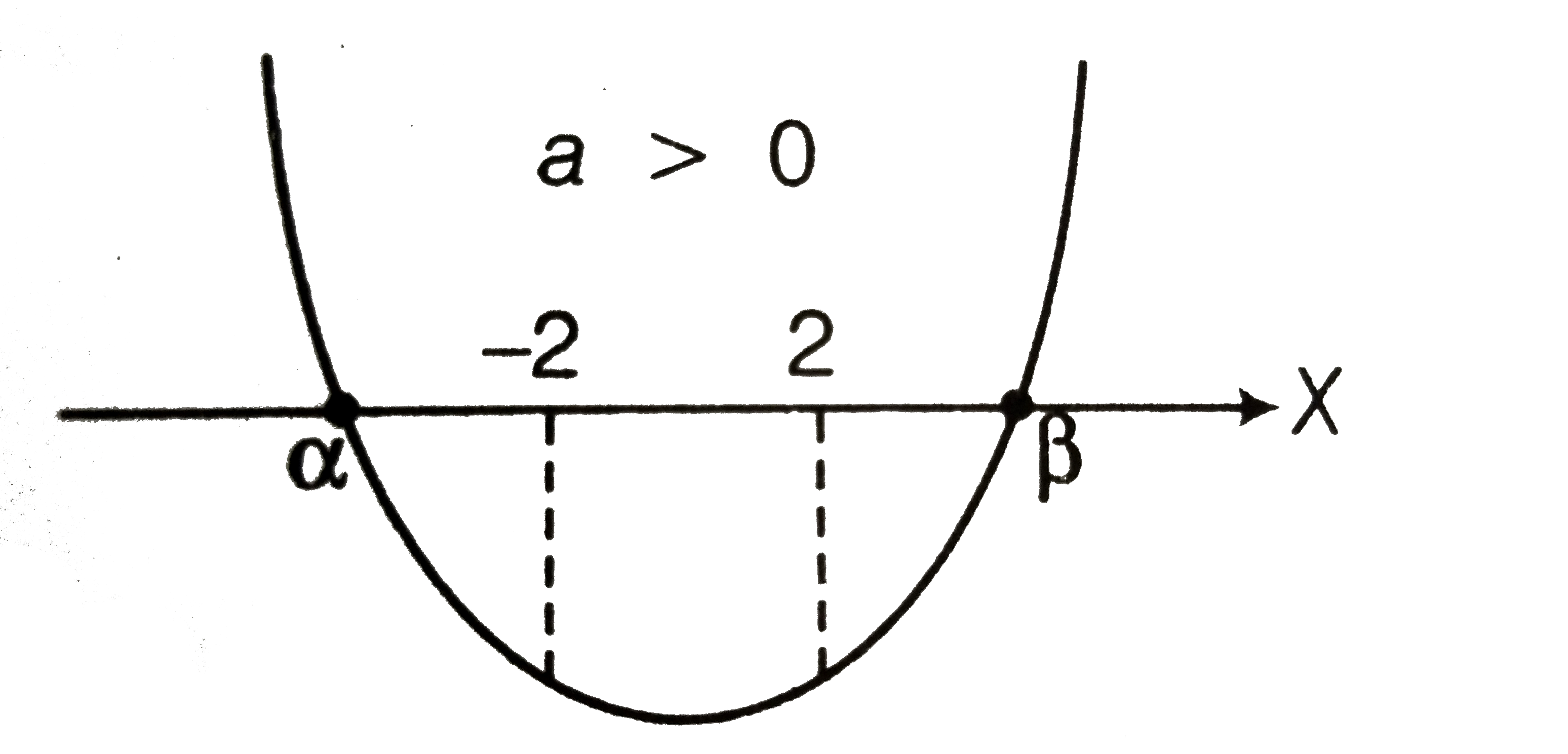
b2−4ac>0
or b2>4ac…… i and f(0)<0
⇒c<0..ii
f(1)<0
⇒a+b+c<0………iii
f(−1)<0
⇒a−b+c<0………..iv
f(2)<0
⇒4a+2b+c<0………v
f(−2)<0
⇒4a−2b+c<0...............vi
From Eqs i and ii we get
c<0,b2−4ac>0
From Eqs. (iii) and (iv) we get
a−|b|+c<0
and from Eqs (v) and (vi) we get
4a−2|b|+c<0
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:ARIHANT MATHS ENGLISHChapter:THEORY OF EQUATIONSExercise:Exercise (Passage Based Questions)
Explore 21 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHS ENGLISHChapter:THEORY OF EQUATIONSExercise:Exercise (Single Integer Answer Type Questions)
Explore 10 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHS ENGLISHChapter:THEORY OF EQUATIONSExercise:SCQ_TYPE
Explore 1 Video
- THE STRAIGHT LINESBook:ARIHANT MATHS ENGLISHChapter:THE STRAIGHT LINESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 17 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHS ENGLISHChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
Explore 2 Videos
Similar Questions
Let a,b,c ∈Randa>0. If the quadratic equation ax2+bx+c=0 has two real roots αandβ such that α>−1andβ>1 , then show that 1+∣∣∣ba∣∣∣+ca>0
View SolutionIf a≠0 and the equation ax2+bx+c=0 has two roots αandβ such thet α<−3andβ>2. Which of the following is always true ?
View SolutionIf a, b, c are real if ax2+bx+c=0 has two real roots α,β where a<−1,β>1 then
View SolutionIf α,β are roots of the equation ax2+bx+c=0 then the equation whose roots are 2α+3β and 3α+2β is
View SolutionConsider a quadratic equation ax2+bx+c=0 having roots α,β. If 4a+2b+c>0,a−b+c<0and4a−2b+C>0 then |[α]+[β]| can be {where [] is greatest integer}
View SolutionStatement-1: Ifαandβ are real roots of the quadratic equations ax2+bx+c=0and−ax2+bx+c=0, then a2x2+bx+c=0 has a real root between αandβ
Statement-2: If f(x) is a real polynomial and x1,x2∈R such that f(x1)fx2<0, then f(x) = 0 has at leat one real root between x1andx2.
View SolutionIF α,β are the roots of the equation ax2+bx+c=0then the quadratic equation whose roots are α+β,αβ is
View SolutionIn the quadratic equation ax2+bx+c=0, if Δ=b2−4acandα+β,α2+β2,α3+β3 are in GP. where α,β are the roots of ax2+bx+c=0, then
View SolutionIf α,β are the roots of the quadratic equation x2+bx−c=0, the equation whose roots are b and c, is a. x2+αx−β=0 b. x2−[(α+β)+αβ]x−αβ(α+β)=0 c. x2+[(α+β)+αβ]x+αβ(α+β)=0 d. x2+[(α+β)+αβ)]x−αβ(α+β)=0
View SolutionStatement-1 : Let a quadratic equation has a root 3 - 9i then the sum of roots is 6.
and
Statement -2 : If one root of ax2+bx+c=0,a≠0,a,b,c∈R is α+iβ,α,β∈R then the other roots must be α−iβ
View Solution

