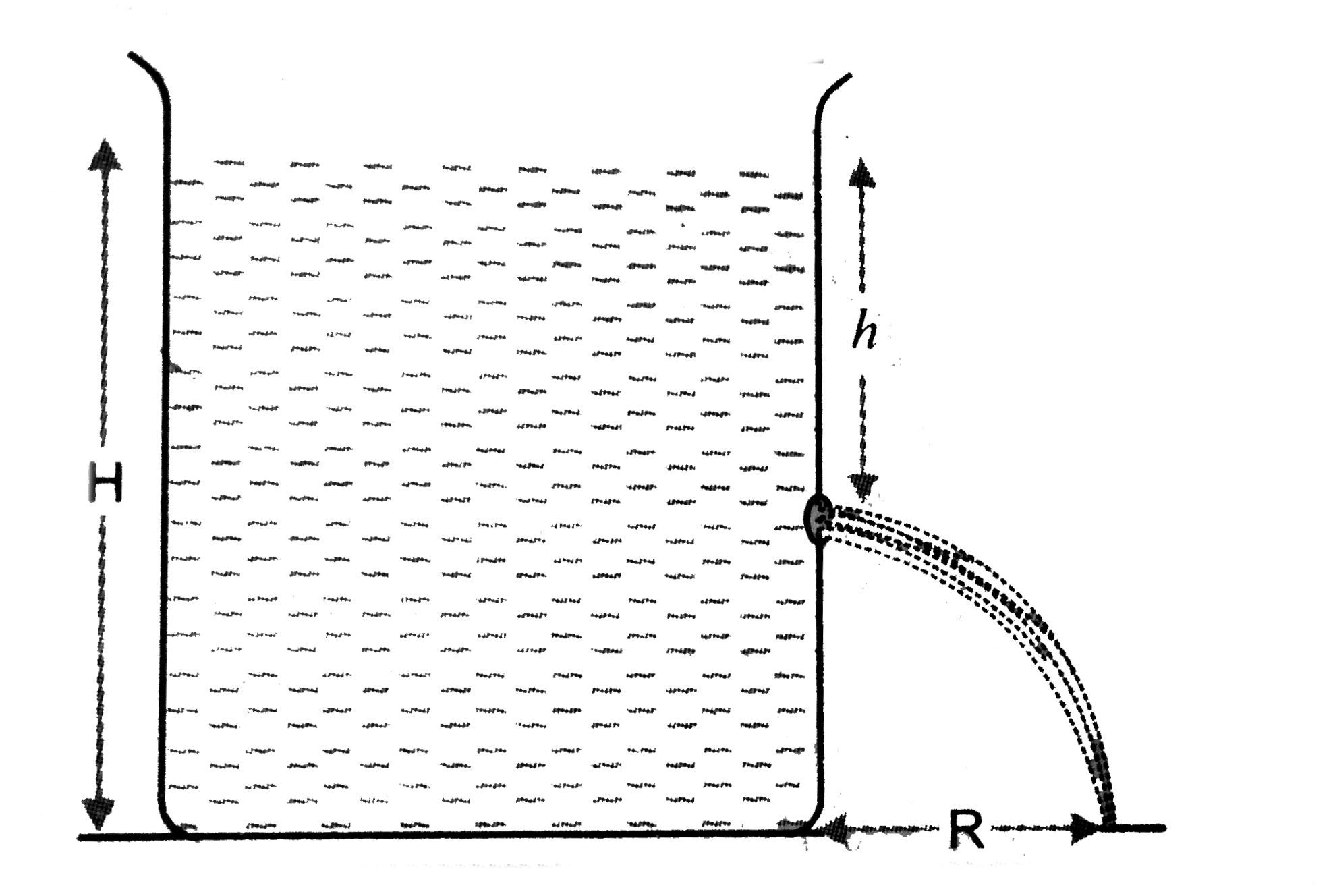
Water stands at a depth H in a tank whose side walls are vertical. A hole is made in one of the walls at a height h below the water surface. The stream of water emerging from the hole strikes the floor at a distance R from the tank, where R is given by
R=√h(H−h)
R=√h(H+h)
R=2√h(H−h)
R=2√h(H+h)
To solve the problem, we need to find the distance R from the tank where the stream of water, emerging from a hole at a height h below the water surface, strikes the floor. We will use the principles of fluid dynamics and projectile motion to derive the expression for R.
1. Determine the velocity of the water exiting the hole:
The velocity v of the water emerging from the hole can be calculated using Torricelli's theorem, which states:
v=√2g(H−h)
where H is the total height of the water column above the hole and h is the height of the hole from the water surface.
Hint: Remember that the potential energy of the water converts to kinetic energy as it exits the hole.
2. Calculate the time of flight t:
The time t it takes for the water to fall from the height h to the ground can be determined using the equation of motion:
h=12gt2
Rearranging this gives:
t=√2hg
Hint: This equation comes from the second equation of motion for free fall.
3. Relate the horizontal distance R to the time of flight and horizontal velocity:
The horizontal distance R that the water travels while falling can be calculated using the formula:
R=v⋅t
Substituting the expressions for v and t:
R=√2g(H−h)⋅√2hg
4. Simplify the expression for R:
Now, we can simplify the expression:
R=√2g(H−h)⋅√2hg=√4h(H−h)
Thus, we have:
R=2√h(H−h)
Hint: Ensure to combine the square roots correctly and factor out constants.
Final Answer:
The distance R from the tank where the stream of water strikes the floor is given by:
R=2√h(H−h)
The velocity v of the water emerging from the hole can be calculated using Torricelli's theorem, which states:
v=√2g(H−h)
where H is the total height of the water column above the hole and h is the height of the hole from the water surface.
The time t it takes for the water to fall from the height h to the ground can be determined using the equation of motion:
h=12gt2
Rearranging this gives:
t=√2hg
The horizontal distance R that the water travels while falling can be calculated using the formula:
R=v⋅t
Substituting the expressions for v and t:
R=√2g(H−h)⋅√2hg
Now, we can simplify the expression:
R=√2g(H−h)⋅√2hg=√4h(H−h)
Thus, we have:
R=2√h(H−h)
The distance R from the tank where the stream of water strikes the floor is given by:
R=2√h(H−h)
Topper's Solved these Questions
Similar Questions
Water stands at a depth H in a tank whose side walls are vertical. A hole is made on one of the walls at a depth h below the water surface. Find at what distance from the foot of the wall does the emerging stream of water strike the floor and for what value of h this range is maximum ? What is the maximum possible range ?
View SolutionWater stands up height H in a tank, whose side walls are vertical. A hole is made on one of the walls does the emerging stream of water strike the floor and for what value of h this range is maximum ?
View Solution
Knowledge Check
A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
 AIF y is increased from zero to H, x will first increase and then decreaseBx is maximum for y=H/2CThe maximum value of x is HDThe maximum value of x will depend on the density of the liquid
AIF y is increased from zero to H, x will first increase and then decreaseBx is maximum for y=H/2CThe maximum value of x is HDThe maximum value of x will depend on the density of the liquidA tank which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank. Choose incorrect option.
 .AIf y is increased from zero to H, x will first increase and then decreaseBx is maximum for y=H/2CThe maximum value of x is HDThe maximum value of x will depend on the density of the liquid.
.AIf y is increased from zero to H, x will first increase and then decreaseBx is maximum for y=H/2CThe maximum value of x is HDThe maximum value of x will depend on the density of the liquid.A water bgarrel having water up to a depth d is placed on a table of height H. A small hole is made on the wall of the barrel at its bollom. If the stream of water comiong out of the hole falls on the ground at a horizontal distance r from the barrel, then the value of d is
A4Hr2B4Hr2Cr24HDH4r2
Water stand at a heigh H in a tank whose sides are vertical. An orifice is made at the depth h on one of the wall Fig. 7(c).25. The emerging stream of water strikes at the distance R from the tank on the floor./ Find the relation for R in term of h, and H. When R is maxmimum, how h and H are related.
View SolutionThe water is filled upto height of 12 m in a tank having vertical sidewalls. A hole is made in one of the walls at a depth 'h' below the water level. The value of 'h' for which the emerging stream of water strikes the ground at the maximum range is ___________m.
View SolutionWater stands at a height of 100 cm in a vessel whose side walls are vertical. A B and C are holes at height 80 cm, 50 cm, and 20 cm respectively from the bottom of the vessel. The correct system of flowing out is:
View SolutionA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
View SolutionA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
View Solution