Water stand at a heigh H in a tank whose sides are vertical. An orifice is made at the depth h on one of the wall Fig. 7(c).25. The emerging stream of water strikes at the distance R from the tank on the floor./ Find the relation for R in term of h, and H. When R is maxmimum, how h and H are related.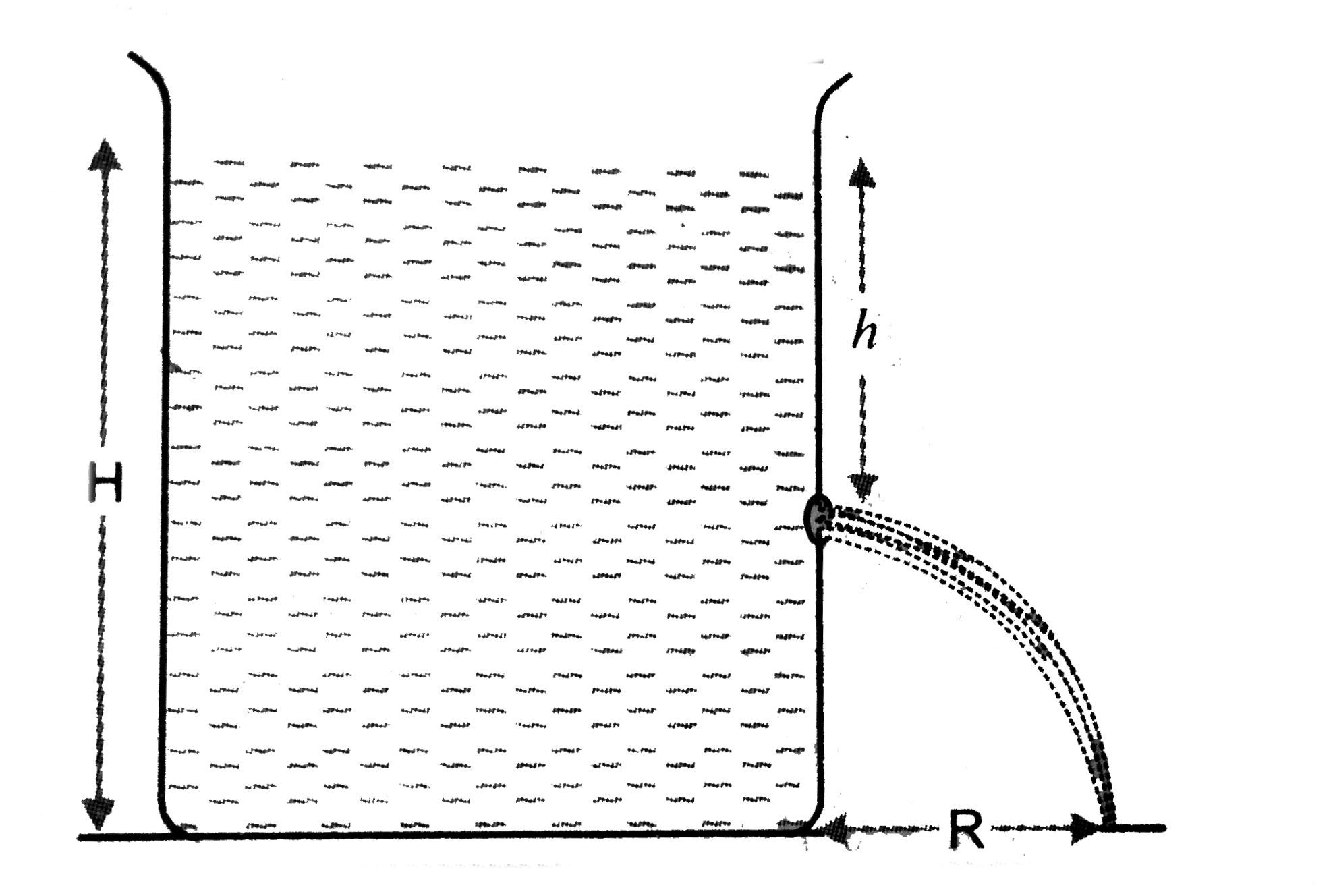 
The correct Answer is:[2√h(H−h);h=H/2]
The velocity with which the liquid flows out of the orifice is v=√2gh or v2=2gh The liquid flowing out of the orifice, becomes a projected horizontally. Height of orifice from ground =(H−h). If is the the time taken by the water to reach the ground, then
t=√2(H−h)lg,
Horizontal range,
R=vt=√2gh×√2(H−h)g=2√h(H−h)
For R to be maximum, dRdh=0
∴dRdh=2×12[h(H−h)]−12ddh(Hh−h2)
=1√h(H−h)9H−2h=0
∴H−2h=0 or h=H/2
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-I
173 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Fill in the Blanks E
10 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Water stands up height H in a tank, whose side walls are vertical. A hole is made on one of the walls does the emerging stream of water strike the floor and for what value of h this range is maximum ?
View SolutionWater stands at a depth H in a tank whose side walls are vertical. A hole is made in one of the walls at a height h below the water surface. The stream of water emerging from the hole strikes the floor at a distance R from the tank, where R is given by
View Solution
Knowledge Check
A water barrel stands on a table of height h. If a small hole is punched in the side of the barrel at its base, it is found that the resultant stream of water strikes the ground at a horizontal distance R from the table. What is the depth of water in the barrel?
AR2hBR22hCR24hD4R2hA tank which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank. Choose incorrect option.
.AIf y is increased from zero to H, x will first increase and then decreaseBx is maximum for y=H/2CThe maximum value of x is HDThe maximum value of x will depend on the density of the liquid.A tank is filled with water up to a height H. Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water. Express the horizontal distance x in terms of H and D
.Ax=√D(H−H)Bx=√D(H−D)2Cx=2√D(H−D)Dx=4√D(H−D)
Water stands at a depth H in a tank whose side walls are vertical. A hole is made on one of the walls at a depth h below the water surface. Find at what distance from the foot of the wall does the emerging stream of water strike the floor and for what value of h this range is maximum ? What is the maximum possible range ?
View SolutionThe water is filled upto height of 12 m in a tank having vertical sidewalls. A hole is made in one of the walls at a depth 'h' below the water level. The value of 'h' for which the emerging stream of water strikes the ground at the maximum range is ___________m.
View SolutionA water barrel stands on a table of height h.If a small hole is punched in the side of the side of the barrel at its base. It is found that the resultant stream of water striks the ground at a horizontal distance R from the barrel. What is the depth of water in the berrel?
View SolutionFigure shows a stream of fluid emerging from a tube in the base of an open tank. Obtain an expression for 'y' in terms of θ and 'h'. Can exceed 'h'?
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
View Solution