Six point charges (each of magnitude Q) are placed on the six vertices of a cube of side x such that two adjacent vertices are vacant. Electrostatic field intensity at the centre of the cube is (k=14πε0)
4√2√3kQx2
8√25√3kQx2
8√23√3kQx2
4√25√3kQx2
To find the electrostatic field intensity at the center of a cube with six point charges placed at its vertices, we can follow these steps:
1. Understanding the Geometry of the Cube:
- A cube has 8 vertices. In this case, 6 vertices are occupied by point charges of magnitude Q, and 2 adjacent vertices are vacant.
2. Positioning the Charges:
- Let's denote the vertices of the cube as A,B,C,D,E,F,G,H.
- Assume the charges +Q are placed at vertices A,B,C,D,E,F, while vertices G and H are vacant.
3. Finding the Center of the Cube:
- The center of the cube is equidistant from all vertices. The distance from any vertex to the center O of the cube can be calculated using the formula for the diagonal of the cube:
Distance from vertex to center=√3x2
4. Calculating the Electric Field Due to Each Charge:
- The electric field E due to a point charge Q at a distance r is given by:
E=kQr2
- For our case, the distance r from each charge to the center is √3x2. Thus, the electric field due to each charge +Q at the center is:
E=kQ(√3x2)2=4kQ3x2
5. Considering the Symmetry:
- Since the charges are symmetrically placed, the net electric field due to the six +Q charges at the center will cancel out to zero.
6. Calculating the Contribution from the Vacant Vertices:
- The vacant vertices G and H would have had charges −Q if they were present. The electric field due to a charge −Q at the center is:
E−Q=−4kQ3x2
- Since there are two vacant vertices, the total electric field contribution from these would be:
Etotal=2×−4kQ3x2=−8kQ3x2
7. Resultant Electric Field:
- The resultant electric field at the center of the cube due to the vacant vertices is:
Eresultant=−8kQ3x2
Final Answer:
The electrostatic field intensity at the center of the cube is:
E=−8kQ3x2
- A cube has 8 vertices. In this case, 6 vertices are occupied by point charges of magnitude Q, and 2 adjacent vertices are vacant.
- Let's denote the vertices of the cube as A,B,C,D,E,F,G,H.
- Assume the charges +Q are placed at vertices A,B,C,D,E,F, while vertices G and H are vacant.
- The center of the cube is equidistant from all vertices. The distance from any vertex to the center O of the cube can be calculated using the formula for the diagonal of the cube:
Distance from vertex to center=√3x2
- The electric field E due to a point charge Q at a distance r is given by:
E=kQr2
- For our case, the distance r from each charge to the center is √3x2. Thus, the electric field due to each charge +Q at the center is:
E=kQ(√3x2)2=4kQ3x2
- Since the charges are symmetrically placed, the net electric field due to the six +Q charges at the center will cancel out to zero.
- The vacant vertices G and H would have had charges −Q if they were present. The electric field due to a charge −Q at the center is:
E−Q=−4kQ3x2
- Since there are two vacant vertices, the total electric field contribution from these would be:
Etotal=2×−4kQ3x2=−8kQ3x2
- The resultant electric field at the center of the cube due to the vacant vertices is:
Eresultant=−8kQ3x2
The electrostatic field intensity at the center of the cube is:
E=−8kQ3x2
Topper's Solved these Questions
Similar Questions
Eight point charges , each q , are placed on the vertices of a cube of side a. Find the potential energy of the system of charges.
View SolutionFour charges of same magnitude and same sign are placed at the corners of a square, of each side0⋅1m. What is electric field intensity at the center of the square?
View Solution
Knowledge Check
- Question 1 - Select One or More
Five point charges each of charge + q are placed on five vertices of a regular of side h as shown in the figure. Then
Athe forces on (-q) at O due to charges +q at A and D are balanced.Bthe forces on (-q) due to charges at D and E are balanced.CThe resultant force on −q at O is 14πε0q2h2 along OE.DThe resultant force on - q at O is 14πε0q2h2 along OC. - Question 2 - Select One
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2 - Question 3 - Select One
Three point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2
Four identical point charges, each of charge q, are placed on the vertices of a regular hexagon of side a such that the net electric field at centre of hexagon is zero. If one of the charge is now removed, then the electric field at centre of hexagon is k- 4.60
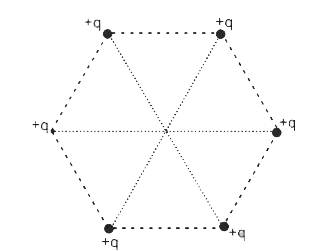
View SolutionSix equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
 View Solution
View SolutionSix equal point charges q each are placed at six corners of a hexago of side a. Find out potential energy of charge system
 View Solution
View SolutionFive point charges, each +q are placed on five vertices of a regular hexagon of side' l '. Find the magnitude of the resultant force on a charge –q placed at the centre of the hexagon.
View SolutionIf 8 identical charges of -g each are placed at the eight corners of a cube of side b, then electrostatic potential energy of a charge +q0 placed at the centre of the cube will be
View Solution

