The reflecting surface is represented by the equation 2x=y2 as shown in the figure. A ray travelling horizontal becomes vertical after reflection. The co-ordinates of the point of incidence are
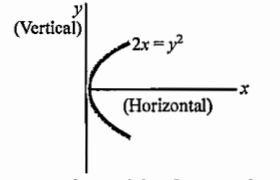
(1/2,1)
(1,1/2)
(1/2, 1/2)
none
Step by step video & image solution for The reflecting surface is represented by the equation 2x =y^2 as shown in the figure. A ray travelling horizontal becomes vertical after reflection. The co-ordinates of the point of incidence are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
When a plane wave front incident on a concave mirror as shown in figure then shape of reflected wave front just after reflection :-

View SolutionA prism has refracting angle 30∘ and μ=2. One of the mat surface of the prism is polished to make it reflecting. Find the incidence angle of a light ray on other mat surface of prism so that after reflection the ray will retrace the path of incident ray.
View Solution
Knowledge Check
A reflecting surface is represented by the equation
y=2Lπsin(πxL), where 0≤x≤L. A ray of light travelling horizontally becomes vertical after reflection with the surface. The co-ordinates of the point where this ray is incident is.
 A(L4,√2Lπ)B(L3,√3Lπ)C(3L4,√2Lπ)D(2L3,√3Lπ)
A(L4,√2Lπ)B(L3,√3Lπ)C(3L4,√2Lπ)D(2L3,√3Lπ)A refracting surface is represented by the equation x2+y2=a2. A ray travelling in negative x-directed towards positive y-direction after reflection from the surface at point P. Then co-ordinates of point P are
 A(0.8 a, 0.6 a)B(0.6 a, 0.8 a)C(a2,a2)DNone of these
A(0.8 a, 0.6 a)B(0.6 a, 0.8 a)C(a2,a2)DNone of theseThe reflective surface is given by y=2sinx. The reflective surface is facing positive axis. What is the least value of coordinate of the point where a ray parallel to positive x-axis becomes parallel to positive y -axis after reflection?
A(π3,√3)B(π2,√2)C(π3,√2)D(π4,√3)
A horizontal ray of light passes through a prism whose apex angle is 4∘ and then strikes a vertical mirror M as shown in Figure. For the ray to become horizontal after reflection, Find the angle by which the mirror must be rotated.
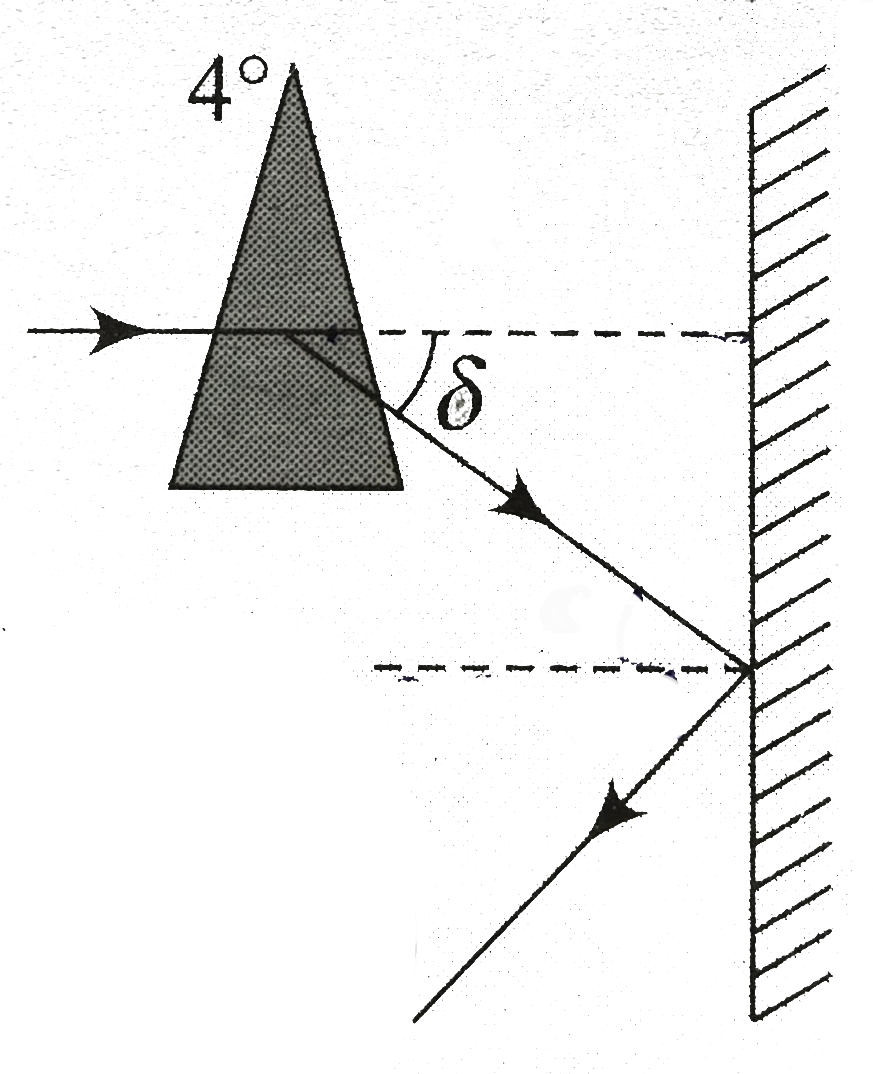
View SolutionA ray of light, travelling parallel to diameter of a sphere enters the sphere through a hole at point A as shown in the figure. The inner surface of the sphere is made perfectly reflecting. Find the number of reflections suffered by the ray before coming out of the sphere.

View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionA horizontal ray of light passes through a prism of index 1.50 and apex angle 4∘ and then strikes a vertical mirror , as shown in the figure. Through what angle must the mirror be rotated if after reflection the ray is to be horizontal?
_E01_041_Q01.png)
View Solution
