A ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
DACB
CDAB
BACD
DBAC
The correct Answer is:C
Note down the given angle, i.e., the angle between the incident light ray and the plane mirror. Draw a normal line on the plane mirror at the point of incidence. The sum of the angle between the normal and the incident light ray and the angle between the plane mirror and the incident light ray is 90∘ . From this, determine the angle of incidence. From the laws of reflection the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
Topper's Solved these Questions
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - ASSESSMENT TEST (TEST 1 (SELECT THE CORRECT ALTERNATIVE)
15 Videos
- KINEMATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICSEXERCISE - ASSESSMENT TEST (TEST 2 (SELECT THE CORRECT ALTERNATIVE)
15 Videos
- MACHINES AND TOOLSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MACHINES AND TOOLSEXERCISE - CONCEPT APPLICATION (LEVEL 2)
12 Videos
Similar Questions
If the angle of incidence on a plane mirror is 30∘, then angle between the reflected ray and the plane mirror is _____
View SolutionA light ray is incident on a plane mirror making an angle of 45∘ with respect to the surface of the mirror. The value of the angle between incident ray and reflected ray is ____∘
View Solution
Knowledge Check
A ray of light is incident at an angle of 35∘ on a plane mirror. What is angle θ ?
 A35∘B45∘C55∘Dnone of these
A35∘B45∘C55∘Dnone of theseA ray of light is incident at an angle of 35∘ on a plane mirror. What is the angle between the incident and the reflected rays ?
A90∘B100∘C110∘Dnone of theseA ray of light is incident on a plane mirror at an angle of incidence of 30∘. The deviation produced by the mirror is
A30∘B60∘C90∘D120∘
A light ray is incident on a plane mirror making an angle of 90∘ with the mirror's surface. The angle of reflection of the light is _______ .
View SolutionA light ray is incident on a plane mirror making an angle of 90∘ with the mirror's surface. The angle of reflection of the light is _______ .
View SolutionIf a light ray incident on a plane mirror makes an angle 30∘ with it, find the angle of incidence and angle of reflection.
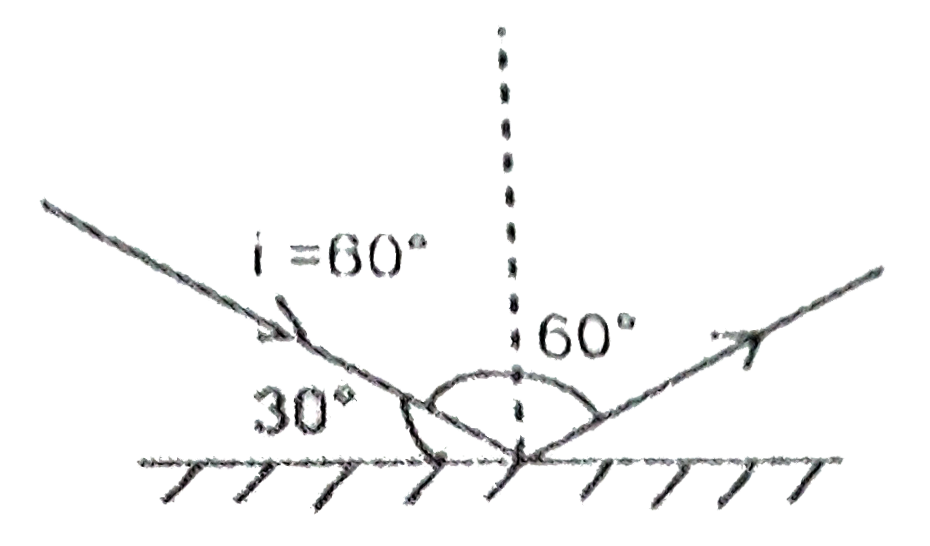
View SolutionIf a light ray incident on a plane mirror makes an angle 30∘ with it, find the angle of incidence and angle of reflection.

View SolutionA ray of light is incident normally on a plane mirror. The angle of reflection will be
View Solution
