If the frequency of the incident radiation is increased from 4×1015Hz to 8×1015Hz. by how much will the stopping potential for a given photo-sensitive surface go up ?
To solve the problem step by step, we will use the photoelectric effect principles and the relationship between frequency, stopping potential, and kinetic energy.
Step 1: Identify the given frequencies
We have two frequencies:
- ν1=4×1015Hz
- ν2=8×1015Hz
Step 2: Write the formula for kinetic energy
The kinetic energy (KE) of the emitted electrons can be expressed as:
KE=hν−hν0
where h is Planck's constant and ν0 is the threshold frequency.
Step 3: Write the kinetic energy equations for both frequencies
For the first frequency ν1:
KE1=hν1−hν0
For the second frequency ν2:
KE2=hν2−hν0
Step 4: Relate kinetic energy to stopping potential
The kinetic energy can also be expressed in terms of stopping potential V:
KE=eV
where e is the charge of an electron. Therefore, we can write:
eV1=hν1−hν0(1)
eV2=hν2−hν0(2)
Step 5: Subtract the two equations
Subtract equation (1) from equation (2):
eV2−eV1=(hν2−hν0)−(hν1−hν0)
This simplifies to:
e(V2−V1)=hν2−hν1
Step 6: Factor out constants
Factoring out h:
e(V2−V1)=h(ν2−ν1)
Step 7: Solve for the change in stopping potential
Now, we can solve for the change in stopping potential:
V2−V1=h(ν2−ν1)e
Step 8: Substitute the known values
Using h=6.626×10−34Js and e=1.6×10−19C:
ν2−ν1=8×1015−4×1015=4×1015Hz
Substituting these values:
V2−V1=6.626×10−34×4×10151.6×10−19
Step 9: Calculate the change in stopping potential
Calculating the above expression:
V2−V1=6.626×4×10−191.6=26.504×10−191.6≈16.65V
Final Answer
The stopping potential will increase by approximately 16.65V.
---
We have two frequencies:
- ν1=4×1015Hz
- ν2=8×1015Hz
The kinetic energy (KE) of the emitted electrons can be expressed as:
KE=hν−hν0
where h is Planck's constant and ν0 is the threshold frequency.
For the first frequency ν1:
KE1=hν1−hν0
For the second frequency ν2:
KE2=hν2−hν0
The kinetic energy can also be expressed in terms of stopping potential V:
KE=eV
where e is the charge of an electron. Therefore, we can write:
eV1=hν1−hν0(1)
eV2=hν2−hν0(2)
Subtract equation (1) from equation (2):
eV2−eV1=(hν2−hν0)−(hν1−hν0)
This simplifies to:
e(V2−V1)=hν2−hν1
Factoring out h:
e(V2−V1)=h(ν2−ν1)
Now, we can solve for the change in stopping potential:
V2−V1=h(ν2−ν1)e
Using h=6.626×10−34Js and e=1.6×10−19C:
ν2−ν1=8×1015−4×1015=4×1015Hz
Substituting these values:
V2−V1=6.626×10−34×4×10151.6×10−19
Calculating the above expression:
V2−V1=6.626×4×10−191.6=26.504×10−191.6≈16.65V
The stopping potential will increase by approximately 16.65V.
Similar Questions
(a) (i) Write Einstein.s photo electric equation.
(ii) if the frequency of the incident radiation is increased from 4×1015 Hz to 8×1015 Hz by how much will the stopping potential for a given photosensitive surface go up ?
(b) Laser light of wavelength 630 nmis incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits. calculate :
(i) fringe separation i.e., fringr width
(ii) distance of 10th bright fringe from the centre of the interference pattern.
View SolutionSuppose the wavelength of the incident light is increased from 3000Å to 3040Å. Find the corresponding change in the stopping potential. [Take the product hc=12.4×10−7eVm)]
View SolutionIn an experiment of photo-electric effect, the graph of maximum kinetic energy Ek of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in figure below :
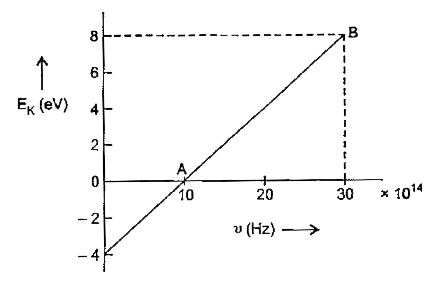
Stopping potential for the photoelectrons emitted by the light of frequency
v=30×1014Hz
View SolutionExplain giving reasons for the following :
(a) Photoelectric current in a photocell increases with the increase in intensity of the incident radiation.
(b) The stopping potential V0 varies linearly with the frequency ν of the incident radiation for a given photosensitive surface with the slope remaining the same for different surfaces.
(c) Maximum kinetic energy of the photoelectrons is independent of the intensity of incident radiation.
View SolutionThe graph between frequency of incident radiations and stopping potential for a given photosensitive material as follows.
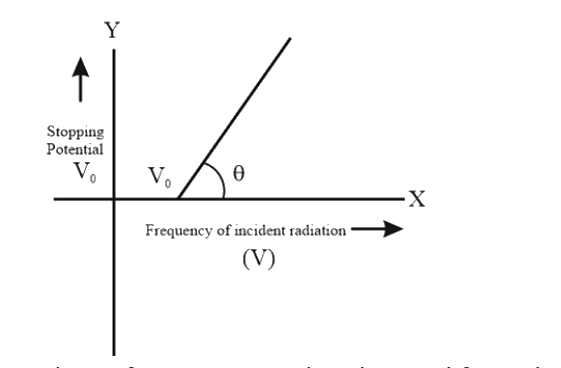
What information can be obtained from the value of the intercept on the potential axis ?
View SolutionThe energy of a photon of frequency 4×1015 Hz is ?
View SolutionGive the ratio of velocities of light rays of frequencies 5×1012Hz and 25×1012Hz
View SolutionThe threshold frequency for photo electric effect for a metal surface is found to be 4.8×1016 Hz. The stopping potential required when the metal is irradiated by radiation of frequency 5.6×1016 Hz is (taking h=6.6×10−34Js and c=1.6×10−19C )
View SolutionIf the frequency of violet radiation is 7.5×1014 Hz, then the value of wavenumber in m−1 for it is p×105. Give the value of p?
View SolutionWhen the electromagnetic radiations of frequencies 4×1015Hz and 6×1015Hz fall on the same metal, in different experiments, the ratio of maximum kinetic energy of electrons liberated is 1:3. The threshold frequency for the metal is
View Solution

