Suppose the wavelength of the incident light is increased from 3000Å to 3040Å. Find the corresponding change in the stopping potential. [Take the product hc=12.4×10−7eVm)]
The correct Answer is:dVs=hce.dλλ2=−hc228e×107=−5.5×10−2volt
To solve the problem of finding the change in stopping potential when the wavelength of the incident light is increased from 3000 Å to 3040 Å, we can follow these steps:
Step 1: Understand the relationship between stopping potential and wavelength
The stopping potential V is related to the energy of the incident photons. The energy of a photon can be expressed as:
E=hcλ
where:
- E is the energy of the photon,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the light.
The stopping potential V is given by the energy of the photon divided by the charge of the electron e:
V=Ee=hceλ
Step 2: Calculate the stopping potential for both wavelengths
We can calculate the stopping potential for both wavelengths λ1=3000Å and λ2=3040Å.
Given:
- hc=12.4×10−7eV m
- Convert wavelengths from Ångströms to meters:
- λ1=3000Å=3000×10−10m
- λ2=3040Å=3040×10−10m
Now, calculate the stopping potential for both wavelengths:
V1=hceλ1=12.4×10−71.6×10−19×3000×10−10
V2=hceλ2=12.4×10−71.6×10−19×3040×10−10
Step 3: Calculate the change in stopping potential
The change in stopping potential ΔV is given by:
ΔV=V1−V2
Step 4: Substitute the values and calculate
1. Calculate V1:
V1=12.4×10−71.6×10−19×3000×10−10≈4.133V
2. Calculate V2:
V2=12.4×10−71.6×10−19×3040×10−10≈4.078V
3. Now, find ΔV:
ΔV=4.133−4.078=0.055V=5.5×10−2V
Final Answer
The change in stopping potential is:
ΔV=5.5×10−2V
---
The stopping potential V is related to the energy of the incident photons. The energy of a photon can be expressed as:
E=hcλ
where:
- E is the energy of the photon,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the light.
V=Ee=hceλ
We can calculate the stopping potential for both wavelengths λ1=3000Å and λ2=3040Å.
- hc=12.4×10−7eV m
- Convert wavelengths from Ångströms to meters:
- λ1=3000Å=3000×10−10m
- λ2=3040Å=3040×10−10m
V1=hceλ1=12.4×10−71.6×10−19×3000×10−10
V2=hceλ2=12.4×10−71.6×10−19×3040×10−10
The change in stopping potential ΔV is given by:
ΔV=V1−V2
1. Calculate V1:
V1=12.4×10−71.6×10−19×3000×10−10≈4.133V
V2=12.4×10−71.6×10−19×3040×10−10≈4.078V
ΔV=4.133−4.078=0.055V=5.5×10−2V
The change in stopping potential is:
ΔV=5.5×10−2V
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise ( Part II : Only one one correct type)
37 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise (2) Only one option correct type
30 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved miscellaneous problems
14 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
Similar Questions
Knowledge Check
When light of wavelength 400nm is incident on the cathode of photocell, the stopping potential recorded is 6V. If the wavelength of the incident light is to 600nm, calculate the new stopping potential. [Given h=6.6×10−34Js,c=3×108m/s,e=1.6×10−19C]
A1.03VB2.42VC4.97VD3.58V
In a photoelectric cell, the wavelength of incident light is chaged from 4000A to 3600A. The change in stopping potential will be
View SolutionIn a photoelectric experiment, the wavelength of the light incident on a metal is changed from 300 nm to 400 nm. Choose the closest value of change in the stopping potential from given options (hce=1240nm.V)
View SolutionIn a photoelectric experiment, the wavelength of the light incident on a metal is changed from 300 nm to 400 nm. Choose the closest value of change in the stopping potential from given options (hce=1240nm.V)
View SolutionIf the frequency of the incident radiation is increased from 4×1015Hz to 8×1015Hz. by how much will the stopping potential for a given photo-sensitive surface go up ?
View SolutionIf wavelength of incident radiation changes from 500nm to 200nm then the maximum kinetic energy increases to 3 times. Find work function ?
View Solution(a) (i) Write Einstein.s photo electric equation.
(ii) if the frequency of the incident radiation is increased from 4×1015 Hz to 8×1015 Hz by how much will the stopping potential for a given photosensitive surface go up ?
(b) Laser light of wavelength 630 nmis incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits. calculate :
(i) fringe separation i.e., fringr width
(ii) distance of 10th bright fringe from the centre of the interference pattern.
View SolutionIn a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ). ) of incident light and the corresponding stopping potential (V0) are given below :
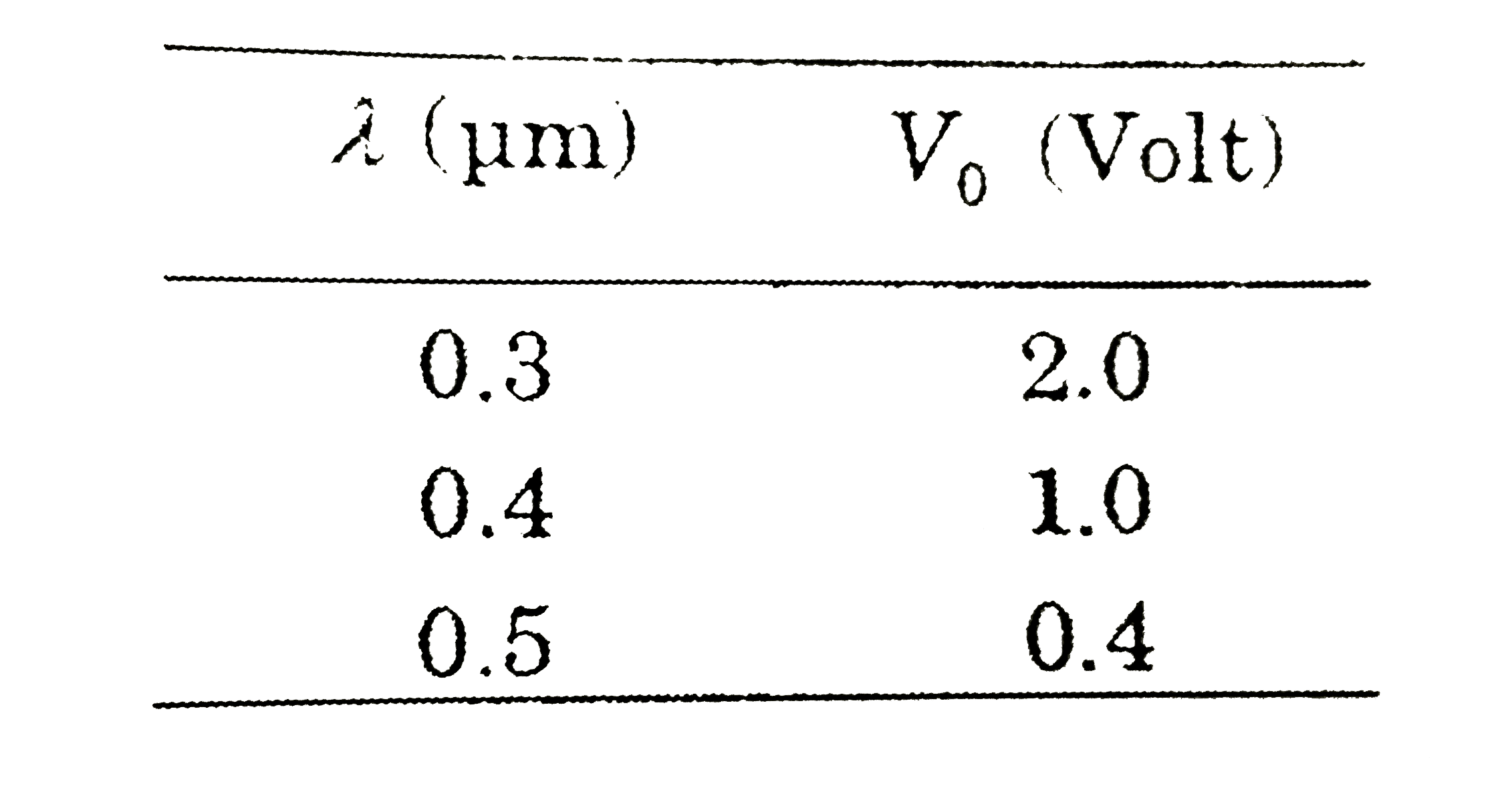
Given that c=3×108ms−1ande=1.6×10−19C Planck's constant (in units of J s) found from such an experiment is
View Solution
