A capacitor, a esistor and a 0.7 H inductor are connected in series to an a.c. supply which generates an emf .e. given by e = 300 sin (200 t) volt. Calculate peak value of the current flowing through the circuit.
To solve the problem step by step, we will calculate the peak value of the current flowing through the circuit with the given components.
Step 1: Identify the given values
- Capacitance C=50μF=50×10−6F
- Resistance R=30Ω
- Inductance L=0.7H
- Peak voltage E0=300V
- Angular frequency ω=200rad/s
Step 2: Calculate the inductive reactance XL
The inductive reactance is given by the formula:
XL=ωL
Substituting the values:
XL=200×0.7=140Ω
Step 3: Calculate the capacitive reactance XC
The capacitive reactance is given by the formula:
XC=1ωC
Substituting the values:
XC=1200×50×10−6=10.01=100Ω
Step 4: Calculate the total impedance Z
The total impedance in a series RLC circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√302+(140−100)2=√302+402=√900+1600=√2500=50Ω
Step 5: Calculate the peak current I0
The peak current can be calculated using Ohm's law for AC circuits:
I0=E0Z
Substituting the values:
I0=30050=6A
Final Answer
The peak value of the current flowing through the circuit is I0=6A.
---
- Capacitance C=50μF=50×10−6F
- Resistance R=30Ω
- Inductance L=0.7H
- Peak voltage E0=300V
- Angular frequency ω=200rad/s
The inductive reactance is given by the formula:
XL=ωL
Substituting the values:
XL=200×0.7=140Ω
The capacitive reactance is given by the formula:
XC=1ωC
Substituting the values:
XC=1200×50×10−6=10.01=100Ω
The total impedance in a series RLC circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√302+(140−100)2=√302+402=√900+1600=√2500=50Ω
The peak current can be calculated using Ohm's law for AC circuits:
I0=E0Z
Substituting the values:
I0=30050=6A
The peak value of the current flowing through the circuit is I0=6A.
Similar Questions
A 20 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
peak value of current in the circuit.
View SolutionA 30 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
The impedance of the circuit and
View SolutionAn ac generator generates an emf .e. given by: e=311sin(100πt) volt. Find the rms value of the emf generated by the generator.
View SolutionA 400 Ω resistor, a 3 H inductor and a 5 μF capacitor are connected in series to a 220 V, 50 Hz ac source. Calculate the :
(1) Impedance of the ciruit.
(ii) Current flowing through the circuit.
View SolutionAn 8 H inductor, a 2 μF capacitor and a 100 Ω resistor are connected in series to an A.C. supply of 220 V and 50 Hz. Calculate :
(i) Impedance of the circuit.
(ii) Current flowing through the circuit.
(iii)Phase difference between the current and the supply voltage.
(iv) Average power consumed by the circuit.
View SolutionA 25(μ)F capacitor, a 0.1 H inductor and a 25Ω resistor are connected in series with an ac source of emf E=310sin314t. Find
(a) the frequency of the emf
(b) the impedance of the circuit
(c) the current in the circuit.
(d) the phase angle
View SolutionA 200Ω resistor and 1H inductor are joined in series with an ac source of emf 10√2sin(200t)V. Calculate the phases difference between emf and current.
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
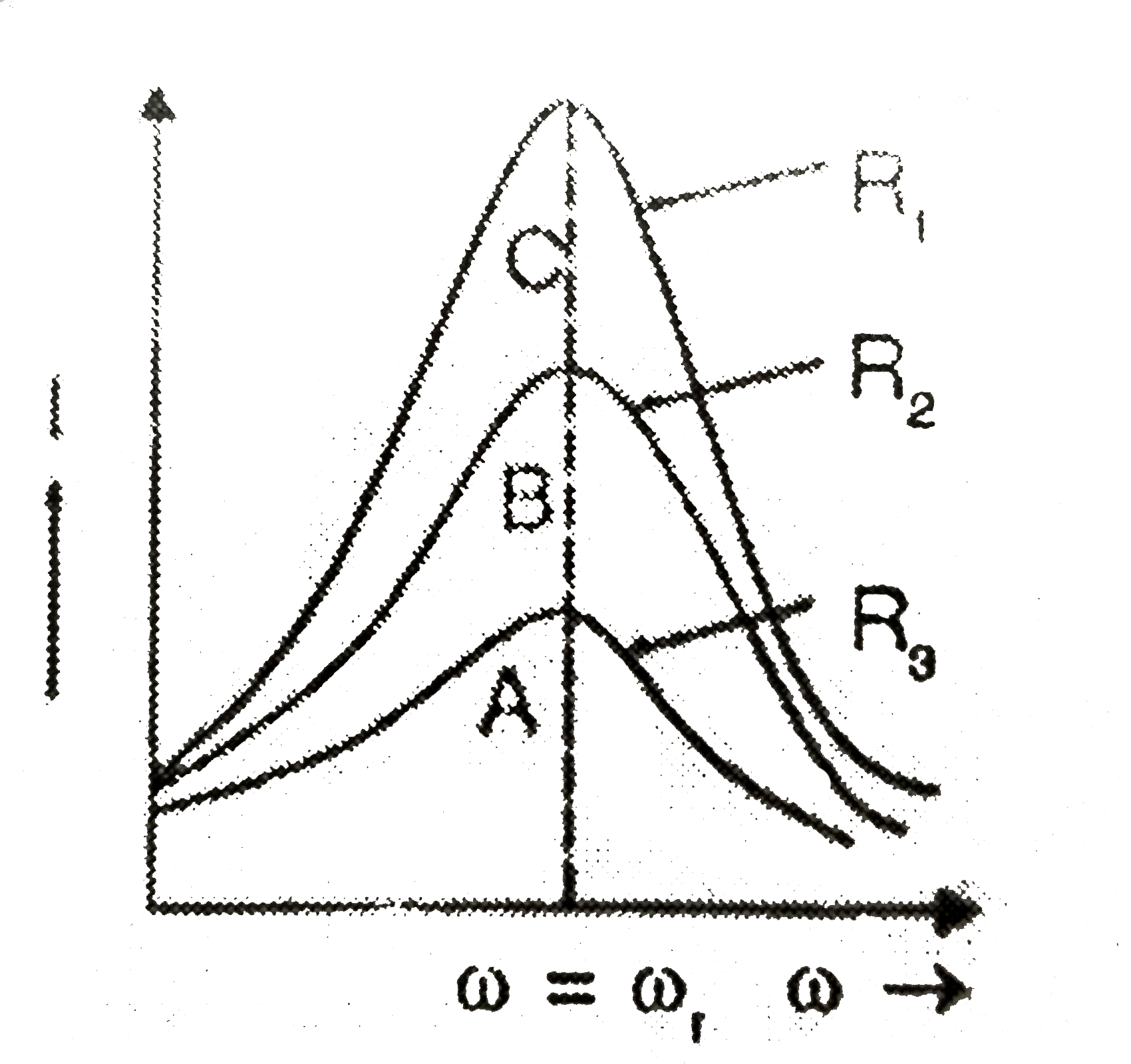
View SolutionA coil of inductance 0.01 H is connected in series with a capacitor of capacitance 25μF with an AC source whose emf is given by E = 310 sin 314t (volt). What is the reactance of the circuit ?
View SolutionIn an ac circuit the current is given by i=0.5sin(314t+60∘) milliampere. Then peak to peak value of current is-
View Solution