A 50 mH inductor is connected across a power supply of emf 130 sin (314 t) volts. Calculate the resistance of the inductor if maximum current in the circuit is 8 A.
The correct Answer is:4.19Ω
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Identify Given Values
- Inductance (L) = 50 mH = 50 × 10^(-3) H
- EMF (V) = 130 sin(314t) volts
- Maximum Current (I₀) = 8 A
- Angular frequency (ω) = 314 rad/s (from the equation of EMF)
Step 2: Calculate Inductive Reactance (Xₗ)
Inductive reactance (Xₗ) is given by the formula:
XL=L⋅ω
Substituting the values:
XL=50×10−3H×314rad/s
Calculating this:
XL=15.7Ω
Step 3: Calculate Maximum Voltage (V₀)
The maximum voltage (V₀) can be taken directly from the EMF equation:
V0=130V
Step 4: Calculate Impedance (Z)
The impedance (Z) of the circuit can be calculated using the formula:
Z=V0I0
Substituting the values:
Z=130V8A
Calculating this:
Z=16.25Ω
Step 5: Relate Impedance, Resistance (R), and Inductive Reactance (Xₗ)
The relationship between impedance (Z), resistance (R), and inductive reactance (Xₗ) in an RL circuit is given by:
Z=√R2+X2L
Substituting the known values:
16.25=√R2+(15.7)2
Step 6: Solve for Resistance (R)
Squaring both sides:
(16.25)2=R2+(15.7)2
Calculating the squares:
264.0625=R2+246.49
Rearranging to find R²:
R2=264.0625−246.49
Calculating:
R2=17.5725
Taking the square root:
R=√17.5725≈4.19Ω
Final Answer
The resistance of the inductor in the circuit is approximately 4.19 Ω.
---
- Inductance (L) = 50 mH = 50 × 10^(-3) H
- EMF (V) = 130 sin(314t) volts
- Maximum Current (I₀) = 8 A
- Angular frequency (ω) = 314 rad/s (from the equation of EMF)
Inductive reactance (Xₗ) is given by the formula:
XL=L⋅ω
Substituting the values:
XL=50×10−3H×314rad/s
Calculating this:
XL=15.7Ω
The maximum voltage (V₀) can be taken directly from the EMF equation:
V0=130V
The impedance (Z) of the circuit can be calculated using the formula:
Z=V0I0
Substituting the values:
Z=130V8A
Calculating this:
Z=16.25Ω
The relationship between impedance (Z), resistance (R), and inductive reactance (Xₗ) in an RL circuit is given by:
Z=√R2+X2L
Substituting the known values:
16.25=√R2+(15.7)2
Squaring both sides:
(16.25)2=R2+(15.7)2
Calculating the squares:
264.0625=R2+246.49
Rearranging to find R²:
R2=264.0625−246.49
Calculating:
R2=17.5725
Taking the square root:
R=√17.5725≈4.19Ω
The resistance of the inductor in the circuit is approximately 4.19 Ω.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CONCEPTUAL QUESTIONS
Explore 25 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:TOUGH & TRICKY PROBLEMS
Explore 12 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
An a.c. voltage of 100 V, 50 Hz is connected across a 20 ohm resistor and 2 mH inductor in series. Calculate ltbr gt (i) impedance of the circuit,
(ii) rms current in the circuit.
View SolutionAn inductor of negligible resistance and a 50 Ω resistor are connnected in series across an AC supply of 100 V. Calculate the voltage across the inductor if voltage across the resistor is 40 V.
View SolutionCalculate the value of inductance of an inductor connected across an alternating power supply of 220 V of frequency 50 Hz such that maximum current flowing through it is 1 A.
View SolutionAn a.c. voltage of 100 V, 50 Hz is connected across a 20 Ω resistance and a 2 mH inductor in series. Calculate (1) impedance of the circuit, (ii) rms current in the circuit.
View SolutionAn inductor of inductance 5 H is connected across an alternating power supply of 220 volts . The frequency of source is 50 Hz. Calculate the maximum value of curent in the inductor .
View SolutionAn inductor of negligible resistance and inductance 1 H is connected across an AC power supply of 200 V . The frequency of source is 50 Hz. Calculate the value of current passing through it.
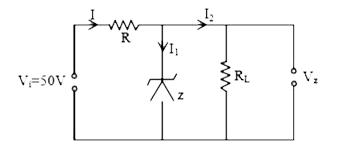
View SolutionIn a given circuit diagram, a 5 V zener diode along with a series resistance is connected across a 50 V power supply. The minimum value of the resistance required, if the maximum zener current is 90 mA will be ___ Ω .
View SolutionA 0.2 H inductor is connected across an AC power supply . The current in the circuit increases from 0 to 3.4 A. Calculate the energy stored in magnetic field of inductor during that period.
View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100Ω. Calculate the time constant. What will be the maximum value of current in the circuit ?
View SolutionA 44 mH inductor is connected to 220 V, 50 Hz a.c. supply. Determine the rms value of the current in the circuit.
View Solution

