In ΔPQR.PS⊥QR.PS=11cmand area of ΔPQR=77sq.cmIfareaofDelta PSQ: areaofDelta PSR = 3:4. f∈dQS and SR.
The correct Answer is:66 cm
To solve the problem step by step, we will follow the information given and apply the concepts of area in triangles.
Step 1: Understand the given information
We have triangle PQR with PS perpendicular to QR. We know:
- PS = 11 cm (height)
- Area of triangle PQR = 77 sq. cm
- The ratio of the areas of triangles PSQ and PSR = 3:4
Step 2: Calculate the total ratio
The total ratio of the areas of triangles PSQ and PSR is:
- 3 (for PSQ) + 4 (for PSR) = 7
Step 3: Find the value of one part of the ratio
Since the total area of triangle PQR is 77 sq. cm, we can find the value of one part of the ratio:
- One part = Total Area / Total Ratio = 77 / 7 = 11 sq. cm
Step 4: Calculate the areas of triangles PSQ and PSR
Now, we can calculate the areas of triangles PSQ and PSR:
- Area of triangle PSQ = 3 * 11 = 33 sq. cm
- Area of triangle PSR = 4 * 11 = 44 sq. cm
Step 5: Use the area formula for triangle PSQ
The area of triangle PSQ can be expressed using the formula:
Area=12×base×height
Substituting the known values:
33=12×QS×11
Step 6: Solve for QS
Rearranging the equation:
33=112×QS
Multiply both sides by 2:
66=11×QS
Now, divide by 11:
QS=6611=6 cm
Step 7: Use the area formula for triangle PSR
Similarly, for triangle PSR:
44=12×SR×11
Step 8: Solve for SR
Rearranging the equation:
44=112×SR
Multiply both sides by 2:
88=11×SR
Now, divide by 11:
SR=8811=8 cm
Final Answer
- QS = 6 cm
- SR = 8 cm
---
We have triangle PQR with PS perpendicular to QR. We know:
- PS = 11 cm (height)
- Area of triangle PQR = 77 sq. cm
- The ratio of the areas of triangles PSQ and PSR = 3:4
The total ratio of the areas of triangles PSQ and PSR is:
- 3 (for PSQ) + 4 (for PSR) = 7
Since the total area of triangle PQR is 77 sq. cm, we can find the value of one part of the ratio:
- One part = Total Area / Total Ratio = 77 / 7 = 11 sq. cm
Now, we can calculate the areas of triangles PSQ and PSR:
- Area of triangle PSQ = 3 * 11 = 33 sq. cm
- Area of triangle PSR = 4 * 11 = 44 sq. cm
The area of triangle PSQ can be expressed using the formula:
Area=12×base×height
Substituting the known values:
33=12×QS×11
Rearranging the equation:
33=112×QS
Multiply both sides by 2:
66=11×QS
Now, divide by 11:
QS=6611=6 cm
Similarly, for triangle PSR:
44=12×SR×11
Rearranging the equation:
44=112×SR
Multiply both sides by 2:
88=11×SR
Now, divide by 11:
SR=8811=8 cm
- QS = 6 cm
- SR = 8 cm
Topper's Solved these Questions
Similar Questions
In ΔAST, where TP⊥SA, area equals 204 sq. cm. Given that TP=17cmand area of ΔTSP: area of ΔTAP=3:5, find SP and PA.
View SolutionIn ΔLMN,NT⊥LM. Area of ΔLMN=72sq.mandNT=9cm. If area of ΔNTL, area of ΔNTM=1:3, find LT and TM.
View SolutionIn DetlaABC,AD is perpendicular to BC. If AD = 12 cm, area of ΔADB=90sq.cm. and area of DetlaADB: area De≤taADC=2:3, find BD and DC.

View SolutionIn ΔPQR,PR=8cm,QR=4cmandPL=5cm (Fig 11.22). Find: (i) the area of the ΔPQR (ii) QM
View Solution¯¯¯¯¯¯QR=¯¯¯¯¯RS. If the area of ΔRST is c2, what is the area of ΔQSP ?
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPR
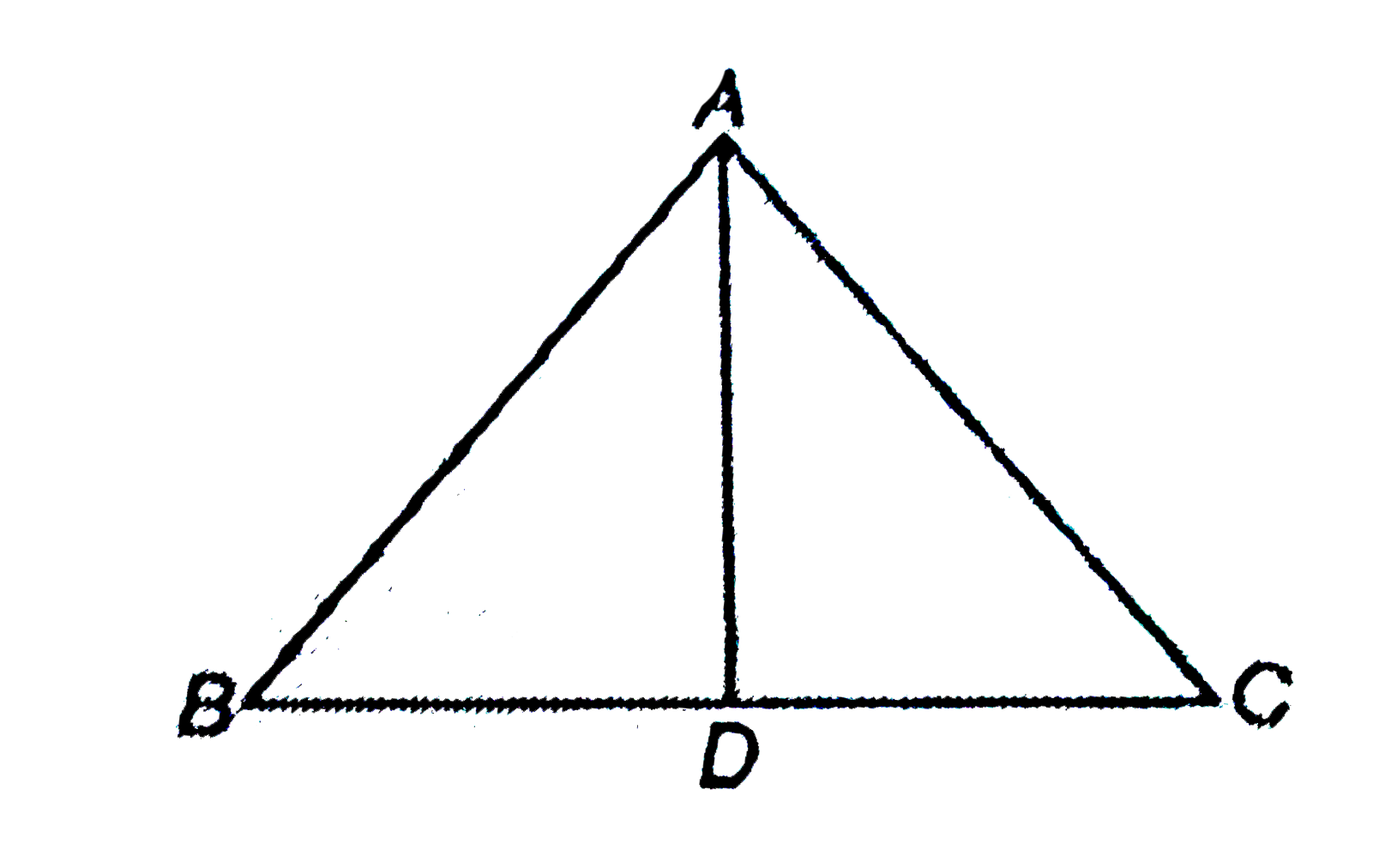
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View SolutionO' is an interior point of a parallelogram ABCD. Prove that :
area of ΔAOB+ area of ΔCOD= area of ΔAOD+ area of ΔBOC
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View Solution

