In Area of If area of area of find LT and TM.
The correct Answer is:
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Understand the problem
We have triangle ΔLMN with a perpendicular NT from point N to line LM. The area of triangle LMN is given as 72sq. m and the height NT=9cm. The areas of triangles NTL and NTM are in the ratio 1:3.
Step 2: Calculate the base LM
The area of triangle LMN can be calculated using the formula:
Area=12×base×height
Substituting the known values:
72=12×LM×9
To find LM, we rearrange the equation:
72=92×LM
Multiplying both sides by 2:
144=9×LM
Now, divide by 9:
LM=1449=16cm
Step 3: Set up the areas of triangles NTL and NTM
Let LT=x and TM=y. From the problem, we know:
x+y=LM=16cm(Equation 1)
The areas of triangles NTL and NTM can be expressed as:
Area of NTL=12×LT×NT=12×x×9=9x2
Area of NTM=12×TM×NT=12×y×9=9y2
Step 4: Set up the ratio of areas
According to the problem, the ratio of the areas of triangles NTL and NTM is 1:3:
9x29y2=13
This simplifies to:
xy=13
From this, we can express y in terms of x:
y=3x(Equation 2)
Step 5: Substitute Equation 2 into Equation 1
Substituting y=3x into x+y=16:
x+3x=16
4x=16
Dividing both sides by 4:
x=4cm
Step 6: Find y
Now, substituting x back into Equation 2 to find y:
y=3x=3×4=12cm
Final Answer:
Thus, the lengths are:
- LT=4cm
- TM=12cm
We have triangle ΔLMN with a perpendicular NT from point N to line LM. The area of triangle LMN is given as 72sq. m and the height NT=9cm. The areas of triangles NTL and NTM are in the ratio 1:3.
The area of triangle LMN can be calculated using the formula:
Area=12×base×height
Substituting the known values:
72=12×LM×9
To find LM, we rearrange the equation:
72=92×LM
Multiplying both sides by 2:
144=9×LM
Now, divide by 9:
LM=1449=16cm
Let LT=x and TM=y. From the problem, we know:
x+y=LM=16cm(Equation 1)
The areas of triangles NTL and NTM can be expressed as:
Area of NTL=12×LT×NT=12×x×9=9x2
Area of NTM=12×TM×NT=12×y×9=9y2
According to the problem, the ratio of the areas of triangles NTL and NTM is 1:3:
9x29y2=13
This simplifies to:
xy=13
From this, we can express y in terms of x:
y=3x(Equation 2)
Substituting y=3x into x+y=16:
x+3x=16
4x=16
Dividing both sides by 4:
x=4cm
Now, substituting x back into Equation 2 to find y:
y=3x=3×4=12cm
Thus, the lengths are:
- LT=4cm
- TM=12cm
Topper's Solved these Questions
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.3
16 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - REVISION EXERCISE
24 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.1
15 Videos
- PERCENTAGE, PROFIT AND LOSSBOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE
26 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - TRY THIS
14 Videos
Similar Questions
Knowledge Check
If ABCD is a square and the area of ΔAFG is 10, then what is the area of ΔAEC ?
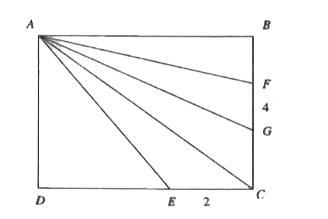 A5B10√2C10√3D10
A5B10√2C10√3D10
In DetlaABC,AD is perpendicular to BC. If AD = 12 cm, area of ΔADB=90sq.cm. and area of DetlaADB: area De≤taADC=2:3, find BD and DC.

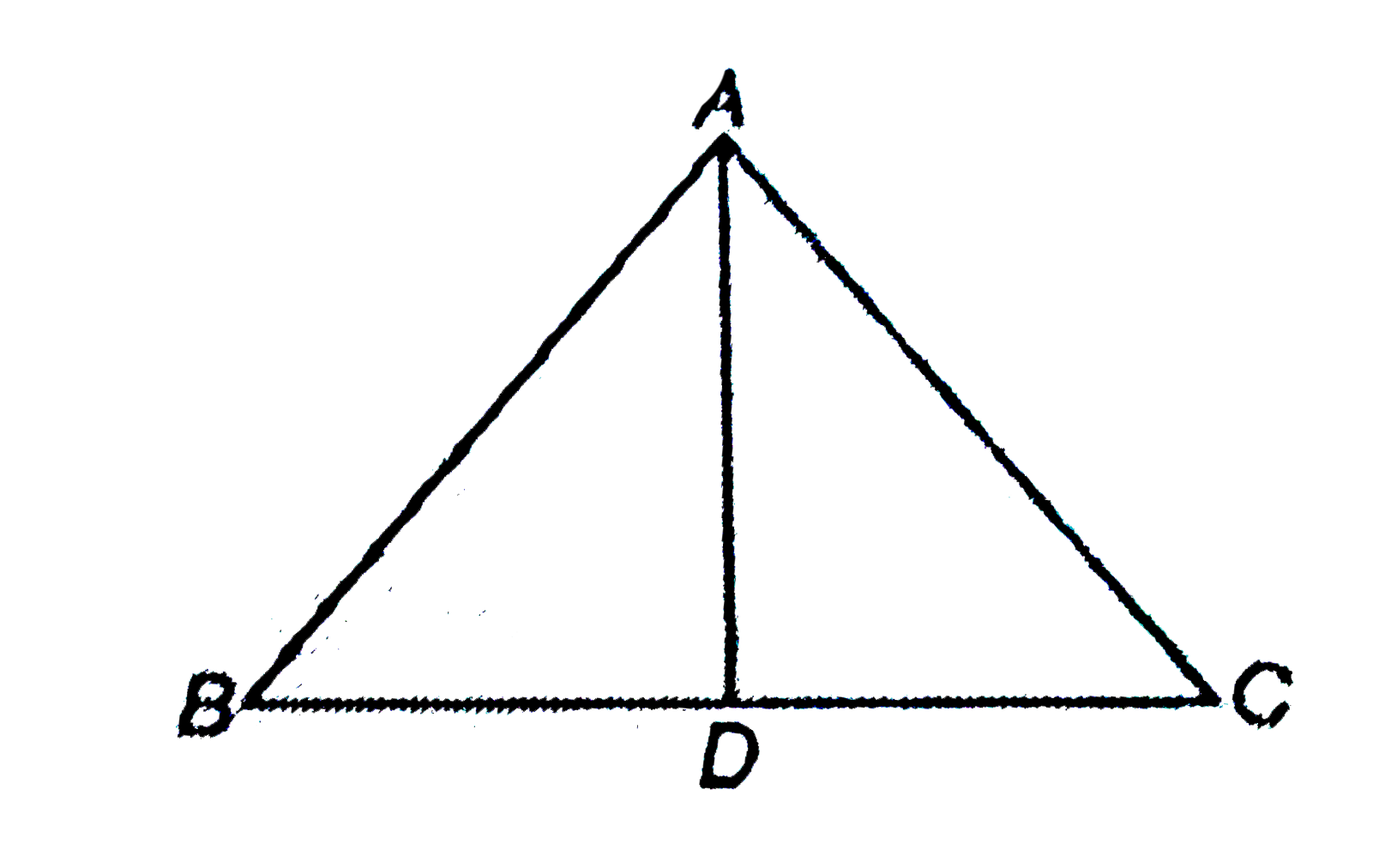
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionAL, BM and CN are perpendicular from angular points of a triangle ABC on the opposite sides BC, CA and AB respectively. Δ is the area of triangle ABC, (r ) and R are the inradius and circumradius.
If area of ΔLMN is Δ', then the value of Δ'Δ is
View SolutionLet the lengths of the altitudes drawn from the vertices of ΔABC to the opposite sides are 2, 2 and 3. If the area of ΔABC is Δ, then find the area of triangle
View SolutionThe area of a triangle is 192 sq.cm and its height is 12 cm. Find its base.
View SolutionO' is an interior point of a parallelogram ABCD. Prove that :
area of ΔAOB+ area of ΔCOD= area of ΔAOD+ area of ΔBOC
View Solution
