PQRS is a parallelogram with ST perpendicular to PQ. Given area of Δ PST = 54 sq.cm, QS = 13 cm, and TQ = 5 cm, find the perimeter of the parallelogram.
The correct Answer is:260sq. Cm
To find the perimeter of the parallelogram PQRS given the area of triangle PST, QS, and TQ, we can follow these steps:
Step 1: Understand the Given Information
We know:
- Area of triangle PST = 54 sq.cm
- QS = 13 cm
- TQ = 5 cm
- ST is perpendicular to PQ.
Step 2: Use the Pythagorean Theorem to Find ST
In triangle SQT, we can apply the Pythagorean theorem since ST is perpendicular to PQ.
SQ2=ST2+TQ2
Substituting the values we know:
132=ST2+52
169=ST2+25
ST2=169−25=144
ST=√144=12 cm
Step 3: Calculate the Base PT of Triangle PST
Using the area formula for triangle PST:
Area=12×base×height
Here, the base is PT and the height is ST.
Substituting the known values:
54=12×PT×12
Solving for PT:
54=6×PT
PT=546=9 cm
Step 4: Find the Length of PQ
Since PQ = PT + TQ:
PQ=PT+TQ=9+5=14 cm
Step 5: Find the Length of PS
Using the Pythagorean theorem again in triangle PST:
PS2=ST2+PT2
Substituting the values:
PS2=122+92
PS2=144+81=225
PS=√225=15 cm
Step 6: Find the Lengths of the Other Sides
Since opposite sides of a parallelogram are equal:
- QR = PS = 15 cm
- RS = PQ = 14 cm
Step 7: Calculate the Perimeter of the Parallelogram
The perimeter (P) of the parallelogram is given by:
P=PQ+QR+RS+SP
Substituting the values:
P=14+15+14+15=58 cm
Final Answer
The perimeter of the parallelogram PQRS is 58 cm.
---
We know:
- Area of triangle PST = 54 sq.cm
- QS = 13 cm
- TQ = 5 cm
- ST is perpendicular to PQ.
In triangle SQT, we can apply the Pythagorean theorem since ST is perpendicular to PQ.
132=ST2+52
169=ST2+25
ST2=169−25=144
ST=√144=12 cm
Using the area formula for triangle PST:
Area=12×base×height
Here, the base is PT and the height is ST.
54=12×PT×12
54=6×PT
PT=546=9 cm
Since PQ = PT + TQ:
PQ=PT+TQ=9+5=14 cm
Using the Pythagorean theorem again in triangle PST:
PS2=ST2+PT2
Substituting the values:
PS2=122+92
PS2=144+81=225
PS=√225=15 cm
Since opposite sides of a parallelogram are equal:
- QR = PS = 15 cm
- RS = PQ = 14 cm
The perimeter (P) of the parallelogram is given by:
P=PQ+QR+RS+SP
Substituting the values:
P=14+15+14+15=58 cm
The perimeter of the parallelogram PQRS is 58 cm.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram DP is perpendicular to AB. Given BD=5cm,AP=3cm.and area of ΔADP=6 sq. cm, find the perimeter of ABCD.
View SolutionABCD is a parallelogram where DE is perpendicular to AB. If BD= 17 cm, AE = 15 cm, and area of ΔADE=60sq. cm, find the perimeter of ABCD.

View SolutionLMNO is a parallelogram where OP is perpenducular to AB. If OM=20cm,LP=9cm, and area of ΔLPO=54sq.cm, find the perimeter of LMNO.
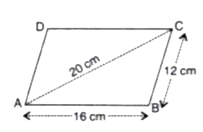
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionIn triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
View SolutionPQRS is a parallelogram with PQ=15cm,ST=10cm,andQV=12cm. Find PS.
View SolutionPQRS is a parallelogram. RA and RB are perpendiculars from R on PQ and PS, respectively. If RA = 15 cm, RB = 22 cm, and QR = 26 cm, find PQ.
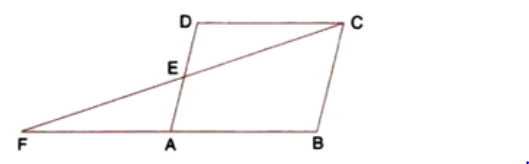
View SolutionThe given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
View SolutionIn figure, ABCD is a parallelogram, AE perpendicular to DC and CF perpendicular to AD. If AB = 16cm, AE = 8cm and CF = 10cm, Find AD.
View SolutionPQRS is a parallegoram whose adjecent sides PQ = 20 cm and QR = 21 cm one of its diagonals QS = 13 cm , find :
the area of the parallelogram PQRS.
View Solution

