LMNO is a parallelogram where OP is perpenducular to AB. If OM=20cm,LP=9cm, and area of ΔLPO=54sq.cm, find the perimeter of LMNO.
The correct Answer is:14.08cm
To find the perimeter of the parallelogram LMNO, we will follow these steps:
Step 1: Find the height OP
We know the area of triangle LPO is given by the formula:
Area=12×base×height
Here, the base LP=9 cm and the area is 54 sq. cm. We can set up the equation:
54=12×9×OP
Multiplying both sides by 2:
108=9×OP
Now, divide both sides by 9:
OP=1089=12 cm
Step 2: Find the length PM using Pythagorean theorem
In triangle PMO, we apply the Pythagorean theorem:
PM2+OP2=OM2
We know OM=20 cm and OP=12 cm. Plugging in the values:
PM2+122=202
This simplifies to:
PM2+144=400
Subtracting 144 from both sides:
PM2=400−144=256
Taking the square root:
PM=√256=16 cm
Step 3: Find the length LM
The length LM can be found by adding LP and PM:
LM=LP+PM=9+16=25 cm
Step 4: Find the length ON
Since opposite sides of a parallelogram are equal, we have:
ON=LM=25 cm
Step 5: Find the length OL using Pythagorean theorem
In triangle LOP, we again apply the Pythagorean theorem:
LP2+OP2=OL2
Substituting the known values:
92+122=OL2
This simplifies to:
81+144=OL2
Thus,
OL2=225
Taking the square root:
OL=√225=15 cm
Step 6: Find the length MN
Since opposite sides of a parallelogram are equal, we have:
MN=OL=15 cm
Step 7: Calculate the perimeter of parallelogram LMNO
The perimeter P of a parallelogram is given by:
P=LM+MN+ON+OL
Substituting the values we found:
P=25+15+25+15=80 cm
Final Answer:
The perimeter of parallelogram LMNO is 80 cm.
---
We know the area of triangle LPO is given by the formula:
Area=12×base×height
Here, the base LP=9 cm and the area is 54 sq. cm. We can set up the equation:
54=12×9×OP
Multiplying both sides by 2:
108=9×OP
Now, divide both sides by 9:
OP=1089=12 cm
In triangle PMO, we apply the Pythagorean theorem:
PM2+OP2=OM2
We know OM=20 cm and OP=12 cm. Plugging in the values:
PM2+122=202
This simplifies to:
PM2+144=400
Subtracting 144 from both sides:
PM2=400−144=256
Taking the square root:
PM=√256=16 cm
The length LM can be found by adding LP and PM:
LM=LP+PM=9+16=25 cm
Since opposite sides of a parallelogram are equal, we have:
ON=LM=25 cm
In triangle LOP, we again apply the Pythagorean theorem:
LP2+OP2=OL2
Substituting the known values:
92+122=OL2
This simplifies to:
81+144=OL2
Thus,
OL2=225
Taking the square root:
OL=√225=15 cm
Since opposite sides of a parallelogram are equal, we have:
MN=OL=15 cm
The perimeter P of a parallelogram is given by:
P=LM+MN+ON+OL
Substituting the values we found:
P=25+15+25+15=80 cm
The perimeter of parallelogram LMNO is 80 cm.
Topper's Solved these Questions
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - UNIT PRACTICE PAPER V
10 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - TRY THIS
41 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.3
16 Videos
- PERCENTAGE, PROFIT AND LOSSBOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE
26 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - TRY THIS
14 Videos
Similar Questions
ABCD is a parallelogram where DE is perpendicular to AB. If BD= 17 cm, AE = 15 cm, and area of ΔADE=60sq. cm, find the perimeter of ABCD.

View SolutionABCD is a parallelogram DP is perpendicular to AB. Given BD=5cm,AP=3cm.and area of ΔADP=6 sq. cm, find the perimeter of ABCD.
View SolutionPQRS is a parallelogram with ST perpendicular to PQ. Given area of Δ PST = 54 sq.cm, QS = 13 cm, and TQ = 5 cm, find the perimeter of the parallelogram.
View SolutionIn the figure, given alongside, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and area of ΔPOB−120cm2. find the area of ΔQOA.

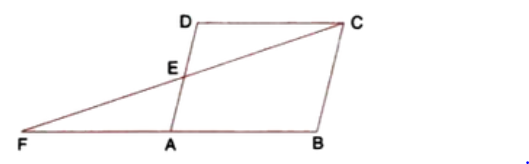
View SolutionThe given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
View SolutionIn triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
View SolutionABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2
Calculate
The area of ΔAPD
View SolutionIf ΔABC~ΔDEF, AB=4cm, DE=6, EF=9 cm and FD=12 cm, then find the perimeter of ΔABC.
View SolutionThe base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.
View SolutionThe area of an equilateral triangle is 36√3 sq. cm. Find its perimeter.
View Solution
