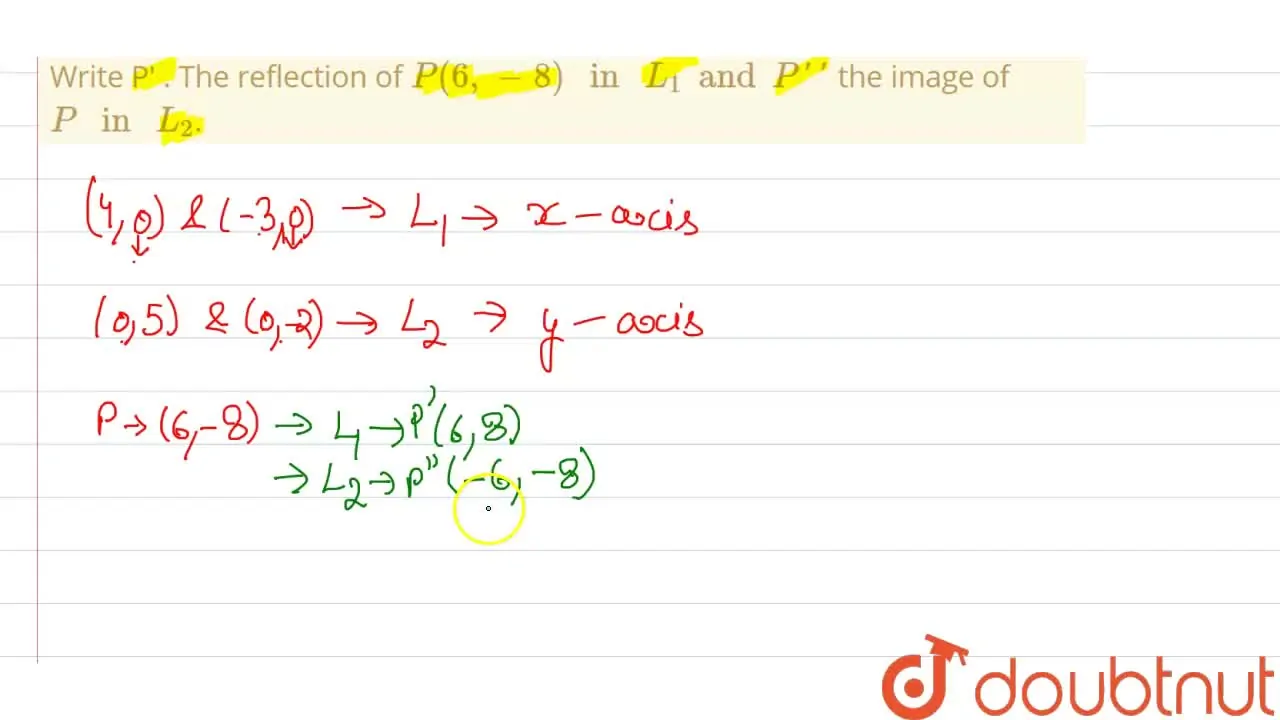
Points (4,0) and (-3,0) are invarient points under reflection in line L1, point (0,5) and (0,-2) are invarient under reflection in line L2.
Write P' . The reflection of P(6,−8) in L1andP'' the image of P in L2.
The correct Answer is:P' = (6.8) and P'' =( -6,-8)
Step by step video, text & image solution for Points (4,0) and (-3,0) are invarient points under reflection in line L_1 , point (0,5) and (0,-2) are invarient under reflection in line L_2. Write P' . The reflection of P(6,-8) " in " L_1 and P'' the image of P " in " L_2. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
Points (4,0) and (-3,0) are invarient points under reflection in line L1, point (0,5) and (0,-2) are invarient under reflection in line L2.
Name and write the equation of lines L1andL2 .View SolutionPoint (-5,0) and (4,0) are invariant point under reflection in the line L1, point (0,-6) and (0,5) are invariant on reflection in the line L2 .
Name or write equation for the line L1andL2 .View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
Name or write equations for the lines L1 and L2View SolutionPoint (-5,0) and (4,0) are invariant point under reflection in the line L1, point (0,-6) and (0,5) are invariant on reflection in the line L2 .
Write down the image of P(2,6) and Q (-8,-3) on reflection in L1 . Name the images as P' and Q' respectively.View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
Write down the images of P (3,4) and Q (-5,-2) on reflection in L2 Name the images as P" and Q" respectively.View SolutionName two invariant points under reflection in the x-axis.
View SolutionPoint (-5,0) and (4,0) are invariant point under reflection in the line L1, point (0,-6) and (0,5) are invariant on reflection in the line L2 .
Write down the image of P and Q on reflection in L2 . Name the images as P'' and Q'' respectively.View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
State or describe a single transformation that maps P' onto P".View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
Write down the images of points P (3, 4) and Q (-5, -2) on reflection in L1 Name the images as P' and Q' respectively.View SolutionPoint (-5,0) and (4,0) are invariant point under reflection in the line L1, point (0,-6) and (0,5) are invariant on reflection in the line L2 .
State or describe a single transformation that maps Q' onto Q'' .View Solution