A solid consisting of a right circular cone, standing on a hemisphere, is placed upright, in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm, the radius of the hemisphere is 2 cm and the height of the cone is 4 cm. Give your answer correct to the nearest centimetre
( Take π=317)
The correct Answer is:136cm3
To solve the problem step by step, we will calculate the volume of the cylinder, the volume of the solid (which consists of a cone and a hemisphere), and then find the volume of water left in the cylinder.
Step 1: Calculate the volume of the cylinder
The formula for the volume of a cylinder is given by:
Vcylinder=πr2h
Where:
- r is the radius of the cylinder
- h is the height of the cylinder
Given:
- Radius of the cylinder r=3 cm
- Height of the cylinder h=6 cm
Substituting these values into the formula:
Vcylinder=π(3)2(6)=π(9)(6)=54π cm3
Step 2: Calculate the volume of the cone
The formula for the volume of a cone is:
Vcone=13πr2h
Where:
- r is the radius of the cone
- h is the height of the cone
Given:
- Radius of the cone r=2 cm
- Height of the cone h=4 cm
Substituting these values into the formula:
Vcone=13π(2)2(4)=13π(4)(4)=163π cm3
Step 3: Calculate the volume of the hemisphere
The formula for the volume of a hemisphere is:
Vhemisphere=23πr3
Where:
- r is the radius of the hemisphere
Given:
- Radius of the hemisphere r=2 cm
Substituting this value into the formula:
Vhemisphere=23π(2)3=23π(8)=163π cm3
Step 4: Calculate the total volume of the solid
The total volume of the solid (cone + hemisphere) is:
Vsolid=Vcone+Vhemisphere=163π+163π=323π cm3
Step 5: Calculate the volume of water left in the cylinder
The volume of water left in the cylinder is calculated by subtracting the volume of the solid from the volume of the cylinder:
Vwater=Vcylinder−Vsolid=54π−323π
To perform this subtraction, we need a common denominator:
54π=1623π
Now, substituting back into the equation:
Vwater=1623π−323π=1303π cm3
Step 6: Substitute π and calculate the final volume
Using π=227:
Vwater=1303×227
Calculating this:
Vwater=130×223×7=286021≈136.19 cm3
Final Answer
Rounding to the nearest centimeter, the volume of water left in the cylinder is approximately:
Volume of water left≈136 cm3
The formula for the volume of a cylinder is given by:
- r is the radius of the cylinder
- h is the height of the cylinder
- Radius of the cylinder r=3 cm
- Height of the cylinder h=6 cm
The formula for the volume of a cone is:
- r is the radius of the cone
- h is the height of the cone
- Radius of the cone r=2 cm
- Height of the cone h=4 cm
The formula for the volume of a hemisphere is:
- r is the radius of the hemisphere
- Radius of the hemisphere r=2 cm
The total volume of the solid (cone + hemisphere) is:
The volume of water left in the cylinder is calculated by subtracting the volume of the solid from the volume of the cylinder:
Using π=227:
Rounding to the nearest centimeter, the volume of water left in the cylinder is approximately:
Topper's Solved these Questions
Similar Questions
A solid consisting of a right standing on a hemisphere is placed upright in a right circular cylinder full of water and touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm, the radius of the hemisphere is 60 cm and height of the cone is 120 cm, assuming that the hemisphere and the cone have common base.
View SolutionA solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
View SolutionA solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
View SolutionA solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm.Such that it touhces the bottom .Find the volume of water of left in the cylinder, if the radius of the cylinder is equal to the radius to the cone.

View SolutionThe largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
View SolutionThe largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
View SolutionThe height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find :
the volume
View SolutionThe diameter of the base of a right circular cylinder is 42cm and its height is 10cm. Find the volume of the cylinder.
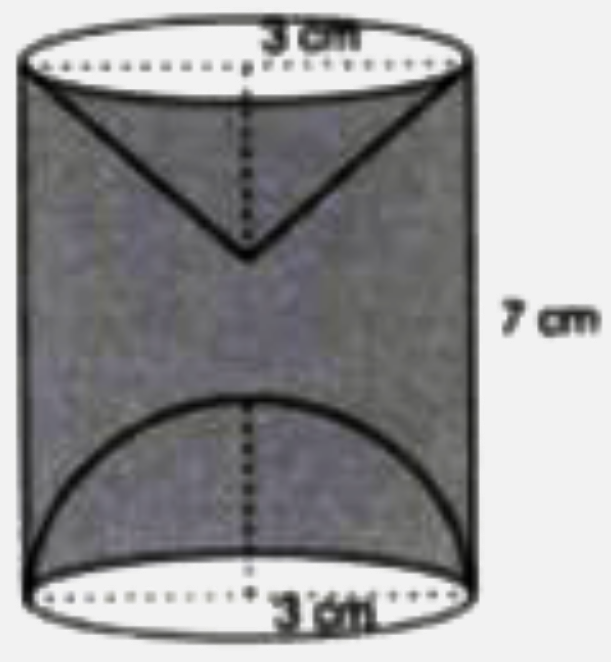
View SolutionA hemispherical and a conical hole are scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as as given alongside :
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number. Take π=227.
View SolutionThe height of a right circular cone is 7 cm and radius is 24 cm. Find the slant height of the cone.
View Solution
