P and Q are two points on the opposite sides of a 90 m high tower AB .The base B, of the tower AB , and points P and Q as observed from top A of tower AB are 60∘and30∘ respectively. Find correct to the nearest .the distance between P and Q.
The correct Answer is:208 m
To find the distance between points P and Q, we can follow these steps:
Step 1: Understand the problem and draw a diagram
We have a tower AB with height 90 m. Points P and Q are on opposite sides of the tower. The angle of depression from point A (top of the tower) to point P is 60 degrees, and to point Q is 30 degrees.
Step 2: Label the diagram
Let's label:
- AB = height of the tower = 90 m
- BP = distance from the base of the tower (B) to point P = x1 m
- BQ = distance from the base of the tower (B) to point Q = x2 m
Step 3: Use trigonometric ratios
From point A, we can use the tangent function for both angles of depression:
1. For angle 60 degrees:
tan(60∘)=ABBP=90x1
We know that tan(60∘)=√3, so:
√3=90x1⟹x1=90√3=30√3 m
2. For angle 30 degrees:
tan(30∘)=ABBQ=90x2
We know that tan(30∘)=1√3, so:
1√3=90x2⟹x2=90√3 m
Step 4: Calculate the total distance between P and Q
The total distance between points P and Q is given by:
PQ=BP+BQ=x1+x2=30√3+90√3=120√3 m
Step 5: Calculate the numerical value
Now, we can calculate the numerical value of PQ:
PQ=120√3≈120×1.732≈207.84 m
Step 6: Round to the nearest meter
Thus, the distance between points P and Q, rounded to the nearest meter, is approximately:
Distance≈208 m
Summary of Steps:
1. Draw a diagram and label the height and distances.
2. Use trigonometric ratios to find x1 and x2.
3. Add x1 and x2 to find the total distance PQ.
4. Calculate the numerical value and round it.
We have a tower AB with height 90 m. Points P and Q are on opposite sides of the tower. The angle of depression from point A (top of the tower) to point P is 60 degrees, and to point Q is 30 degrees.
Let's label:
- AB = height of the tower = 90 m
- BP = distance from the base of the tower (B) to point P = x1 m
- BQ = distance from the base of the tower (B) to point Q = x2 m
From point A, we can use the tangent function for both angles of depression:
1. For angle 60 degrees:
tan(60∘)=ABBP=90x1
We know that tan(60∘)=√3, so:
√3=90x1⟹x1=90√3=30√3 m
tan(30∘)=ABBQ=90x2
We know that tan(30∘)=1√3, so:
1√3=90x2⟹x2=90√3 m
The total distance between points P and Q is given by:
PQ=BP+BQ=x1+x2=30√3+90√3=120√3 m
Now, we can calculate the numerical value of PQ:
PQ=120√3≈120×1.732≈207.84 m
Thus, the distance between points P and Q, rounded to the nearest meter, is approximately:
Distance≈208 m
1. Draw a diagram and label the height and distances.
2. Use trigonometric ratios to find x1 and x2.
3. Add x1 and x2 to find the total distance PQ.
4. Calculate the numerical value and round it.
Topper's Solved these Questions
Similar Questions
There are two points on the horizontal line passing through the foot of a tower in the same side of the tower. The angle of depression of these point from the top of the tower are 45∘ and 60∘ respectively. Find the distance between the two point if the height if the tower is 150 metres.
View SolutionTwo points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60∘ and 45∘ respectively. If the height of the tower is 15 m, then find the distance between these points.
View SolutionTwo men are on the opposite sides of a tower. They measure the angles of elevation of the top of the tower as 45∘ and 30∘ respectively. If the height of the tower is 40 m, then the distance between the men is
View SolutionThe persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30∘and38∘ respectively. Find the distance between them, if the height of the tower is 50 m
View SolutionIn the given figure, A from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
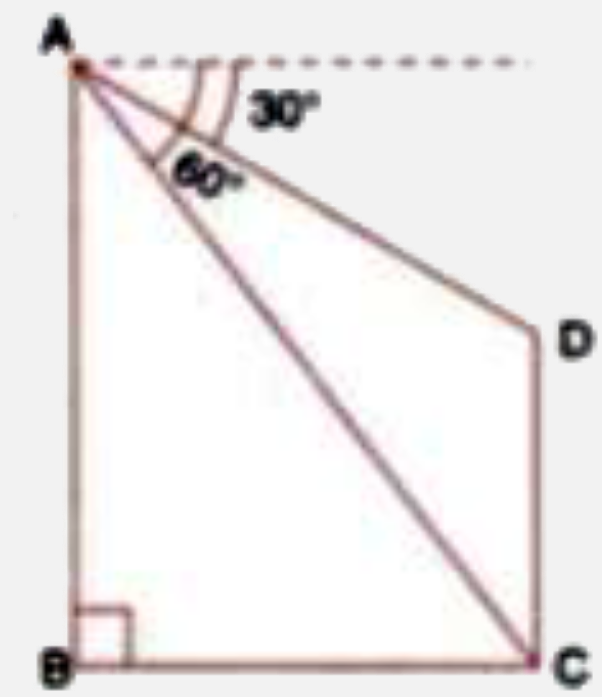
the horizontal distance between AB and CD
View SolutionAt one side of a road, there os a house and on the other side there is a tower. House and tower are on the same horizontal plane. The angle of depression of the top and foot of the house, from the top of the tower are 30∘ and 45∘ respectively. If the height of the house is 10 m, then find the distance between the house and the tower.
View SolutionTwo people standing on the same side of a tower in a straight line with it, measure the angles of elevation of the top of the tower as 25∘and50∘ respectively. If the height of the tower is 70 m, find the distance between the two people
View SolutionThe angles of depression of the and bottom of a 50 m high building from the top of a tower are 45∘ and 60∘ respectively. Find the height of the tower and the horixontal distance between the tower and the building. (Use √3=1.73).
View SolutionTwo man are on the opposite sides of a tower. They measure the angles of elevation the top of the tower as 30∘ and 60∘. If the height of the tower is 150 m, find the distance between the two men.
View SolutionFrom the top of a cliff, the angle of depression of the top and bottom of a tower are observed to be 45∘ and 60∘ respectively. If the height of the tower is 20 m.
Find :
(i) the height of the cliff
(ii) the distance between the cliff and the tower.
View Solution
