Calculate the value of A, if :
(sinA−1)(2cosA−1)=0
The correct Answer is:90∘and60∘
To solve the equation (sinA−1)(2cosA−1)=0, we can break it down into two separate equations:
1. sinA−1=0
2. 2cosA−1=0
Step 1: Solve the first equation
From the first equation, we have:
sinA−1=0
This simplifies to:
sinA=1
Step 2: Find the angle A
The sine function equals 1 at:
A=90∘
Step 3: Solve the second equation
Now, we move to the second equation:
2cosA−1=0
This simplifies to:
2cosA=1
Dividing both sides by 2 gives:
cosA=12
Step 4: Find the angle A
The cosine function equals 12 at:
A=60∘andA=300∘(in the range of 0∘ to 360∘)
Final Solution
Thus, the values of A that satisfy the original equation are:
A=90∘andA=60∘
---
2. 2cosA−1=0
From the first equation, we have:
sinA−1=0
This simplifies to:
sinA=1
The sine function equals 1 at:
A=90∘
Now, we move to the second equation:
2cosA−1=0
This simplifies to:
2cosA=1
Dividing both sides by 2 gives:
cosA=12
The cosine function equals 12 at:
A=60∘andA=300∘(in the range of 0∘ to 360∘)
Thus, the values of A that satisfy the original equation are:
A=90∘andA=60∘
Topper's Solved these Questions
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(B)
34 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -4 ( COMPLEMENTARY ANGLES ) (4 MARKS QUESTIONS )
4 Videos
Similar Questions
Find the magnitude of angle A, if :
2sinAcosA−cosA−2sinA+1=0
View SolutionFind the magnitude of angle A, if :
2sinAcosA−cosA−2sinA+1=0
View SolutionIf cosecA=2, find the value of 1tanA+sinA1+cosA
View SolutionIf cosec A=2 , find the value of 1tanA+sinA1+cosA
View SolutionGiven that 16cotA=12 ; find the value of sinA+cosAsinA−cosA .
View Solution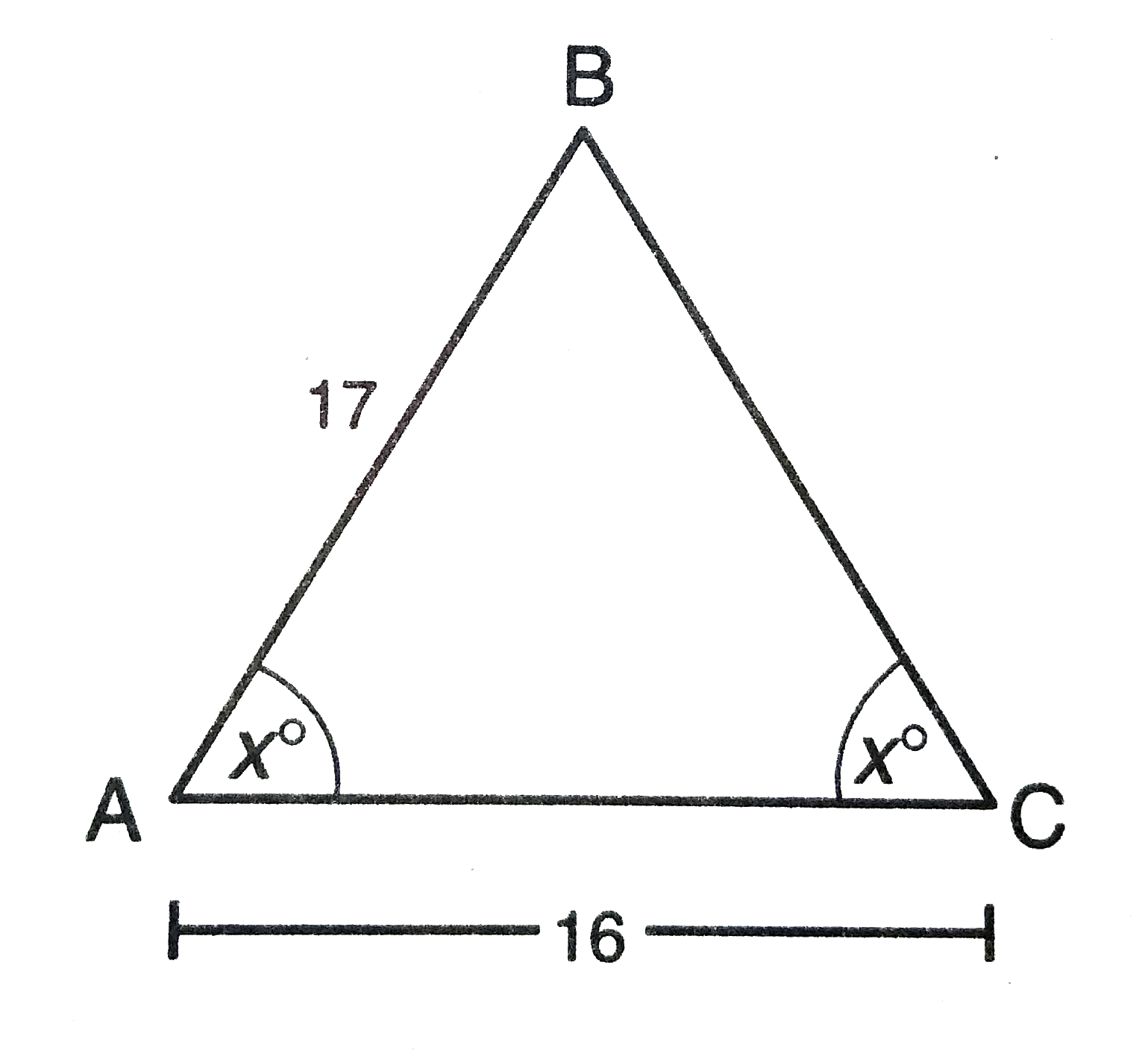
In the figure above, what is the value of sinA−cosA?
View SolutionIn a ΔABC the value of ∠A is given by 5 CosA - 3 = 0 then the equation whose roots are sinA and tanA is :
View SolutionThe value of 2sinAcos3A−2sin3AcosA is
View SolutionIf sinA+cosA=0 and A lies in 4th quadrant, find the values of sinA and cosA.
View SolutionIn a right - angled triangle , it is given that A is an acute angle and tanA=512
cosA+sinAcosA−sinA
View Solution
