A particle in a circular motion covers a distance of 0.5 πr where r is the radius of the circular path. What is the angular displacement ?
The correct Answer is:90∘
To solve the problem of finding the angular displacement of a particle in circular motion that covers a distance of 0.5πr, we can follow these steps:
Step 1: Understand the relationship between linear distance and angular displacement
The relationship between linear distance s traveled by a particle in circular motion and angular displacement θ (in radians) is given by the formula:
s=rθ
where s is the linear distance, r is the radius of the circular path, and θ is the angular displacement in radians.
Step 2: Substitute the given values into the formula
In this problem, we are given that the linear distance s is 0.5πr. We can substitute this value into the formula:
0.5πr=rθ
Step 3: Simplify the equation
Now, we can simplify the equation by dividing both sides by r (assuming r≠0):
0.5π=θ
Step 4: Write the final answer
Thus, the angular displacement θ is:
θ=0.5π radians
Summary
The angular displacement of the particle is 0.5π radians.
---
The relationship between linear distance s traveled by a particle in circular motion and angular displacement θ (in radians) is given by the formula:
s=rθ
where s is the linear distance, r is the radius of the circular path, and θ is the angular displacement in radians.
In this problem, we are given that the linear distance s is 0.5πr. We can substitute this value into the formula:
0.5πr=rθ
Now, we can simplify the equation by dividing both sides by r (assuming r≠0):
0.5π=θ
Thus, the angular displacement θ is:
θ=0.5π radians
The angular displacement of the particle is 0.5π radians.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (VERY SHORT ANSWER QUESTIONS)
Explore 7 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM ANGULAR VELOCITY)
Explore 4 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (LONG ANSWER QUESTIONS)
Explore 8 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
A particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionA charge particle is moving in a uniform magnetic field ib a circular path. The energy of the particle is doubled . If the initial radius of he circular path was R, the radius of the new circular path after the energy is doubled will be
View Solution
Knowledge Check
A particle is moving on a circular path of radius r with uniform speed v. What is the displacement of the particle after it has described an angle of 60∘?
Ar√2Br√3CrD2r
A charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
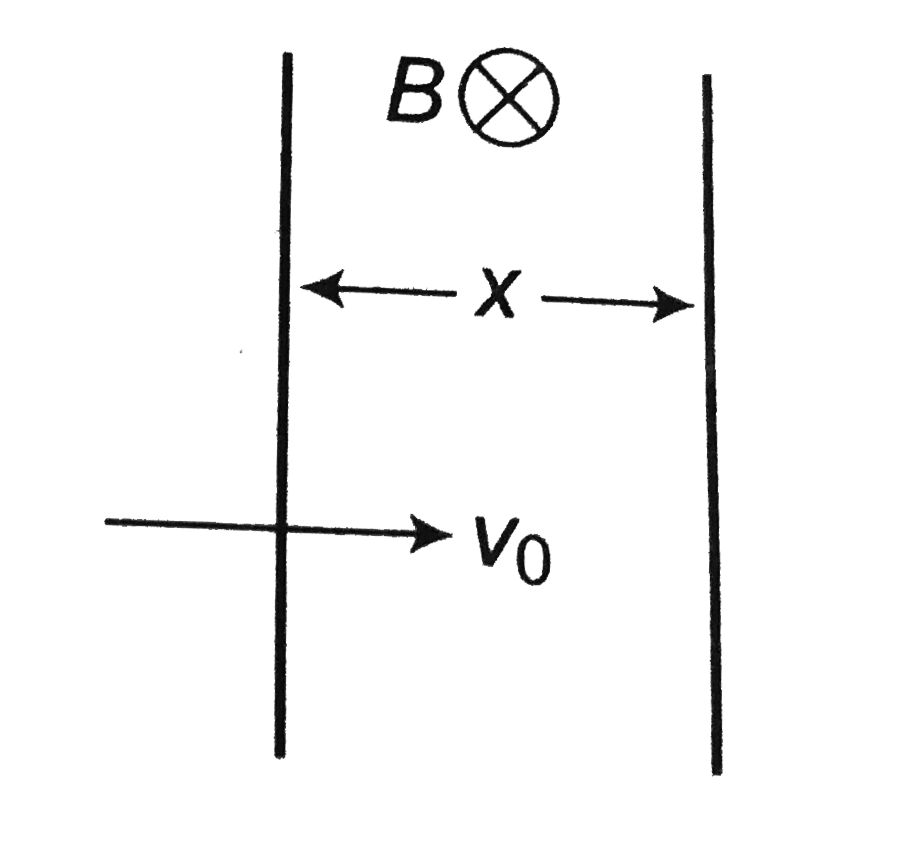
View SolutionThe speed of a body moving in uniform circular motion is doubled and the radius of the circular path is halved. What happens to the centripetal force?
View SolutionA charged particle enters a uniform magnetic field with velocity v0=4m/s perpendicular to it, the length of magnetic field is x=(√32)R, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.
View SolutionIF the equation for the displancement of a particle moving on a circular path is given by θ=2t3+0.5, where θ is in radius and t is in seconds, then the angular velocity of the particle at t=2 s is
View SolutionThe potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by V(r)=kr2/2, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
View SolutionIf the equation for the displacement of a particle moving in a circular path is given by (θ)=2t3+0.5, where θ is in radians and t in seconds, then the angular velocity of particle after 2s from its start is
View SolutionA car is moving in a horizontal level circular track with uniform speed v. If R is the radius of circular path, then the minimum coefficient of friction to avoid over turning is
View Solution

