A,B,C and D are 4 points on the circumference of the circle and O is the centre of circle ∠OBD−∠CBD=∠BDC−∠ODB find ∠A
The correct Answer is:x=60∘
To solve the problem, we need to analyze the given information about the angles formed by points A, B, C, and D on the circumference of the circle with center O.
1. Identify the Angles:
We are given the equation:
∠OBD−∠CBD=∠BDC−∠ODB
Let's denote:
- ∠OBD=x
- ∠CBD=y
- ∠BDC=z
- ∠ODB=w
We can rewrite the equation as:
x−y=z−w
2. Use Properties of Isosceles Triangles:
Since O is the center of the circle, triangles OBD and OBC are isosceles (OB = OD = radius of the circle). Therefore:
∠OBD=∠ODB=x
This means:
w=x
3. Substituting Back:
Substitute w in the equation:
x−y=z−x
Rearranging gives:
2x=y+z
Thus, we can express y in terms of x and z:
y=2x−z
4. Using the Angles in Triangle BCD:
In triangle BCD, the sum of the angles is 180 degrees:
∠BDC+∠CBD+∠CDB=180∘
Substituting the known angles:
z+y+∠CDB=180∘
Using y=2x−z:
z+(2x−z)+∠CDB=180∘
Simplifying gives:
2x+∠CDB=180∘
Therefore:
∠CDB=180∘−2x
5. Finding Angle A:
Since A, B, C, and D are points on the circumference, the angles subtended by the same arc are equal. Therefore:
∠A=∠CDB
Thus:
∠A=180∘−2x
6. Conclusion:
To find a specific value for ∠A, we need additional information about x. However, we have established the relationship:
∠A=180∘−2x
We are given the equation:
∠OBD−∠CBD=∠BDC−∠ODB
Let's denote:
- ∠OBD=x
- ∠CBD=y
- ∠BDC=z
- ∠ODB=w
x−y=z−w
Since O is the center of the circle, triangles OBD and OBC are isosceles (OB = OD = radius of the circle). Therefore:
∠OBD=∠ODB=x
This means:
w=x
Substitute w in the equation:
x−y=z−x
Rearranging gives:
2x=y+z
Thus, we can express y in terms of x and z:
y=2x−z
In triangle BCD, the sum of the angles is 180 degrees:
∠BDC+∠CBD+∠CDB=180∘
Substituting the known angles:
z+y+∠CDB=180∘
Using y=2x−z:
z+(2x−z)+∠CDB=180∘
Simplifying gives:
2x+∠CDB=180∘
Therefore:
∠CDB=180∘−2x
Since A, B, C, and D are points on the circumference, the angles subtended by the same arc are equal. Therefore:
∠A=∠CDB
Thus:
∠A=180∘−2x
To find a specific value for ∠A, we need additional information about x. However, we have established the relationship:
∠A=180∘−2x
Topper's Solved these Questions
Similar Questions
Knowledge Check
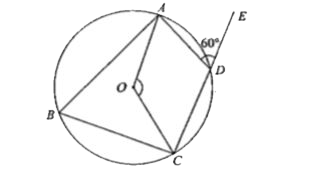
If O is the centre of circle and ∠ADE=60∘ then find ∠AOC
 A60∘B100∘C120∘DNone of these
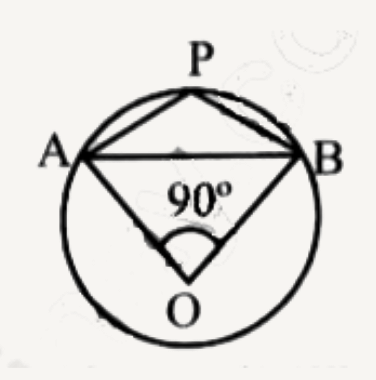
A60∘B100∘C120∘DNone of theseO is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
 A150∘B210∘C75∘D105∘
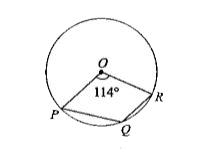
A150∘B210∘C75∘D105∘In the figure, O is the centre of the circle . ∠PQR is equal to
 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘
In the given figure of circle, ‘O’ is the centre of the circle ∠AOB=130∘. What is the value of ∠DMC?
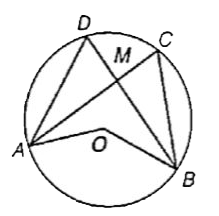
View SolutionIn the diagram , O is the centre of the circle and ∠OPA=30∘, Find ∠ACBand∠ADB respectively.
View SolutionIn the given, figure , O is the centre of the circle and AD is a tangent to the circle at.A if ∠CAD=55∘ and ∠ADC=25∘, then find ∠ABO.

View SolutionWhat is the angle ∠AED if O is the centre of the circle?
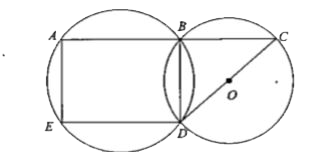
View SolutionIf O is the centre of the circle then find ∠ADC
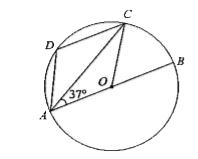
View Solution