There are two chords AB and CD of length 10 cm and 24 cm vespectively both chords are opposed to centre If the distance between chords is 17 cm find radius
The correct Answer is:13 cm
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry
We have two chords AB and CD in a circle. The lengths of the chords are given as:
- Length of AB = 10 cm
- Length of CD = 24 cm
The distance between the two chords is given as 17 cm. We need to find the radius of the circle.
Step 2: Find the Distances from the Center to the Chords
Let O be the center of the circle. The perpendicular distance from the center O to the chord AB is denoted as d1, and the perpendicular distance from O to the chord CD is denoted as d2.
Since the distance between the two chords is 17 cm, we can express this relationship as:
d1+d2=17 cm
Step 3: Use the Length of the Chords to Find Distances
The distance from the center of the circle to a chord can be found using the formula:
d=√r2−(l2)2
where r is the radius of the circle and l is the length of the chord.
For chord AB (length = 10 cm):
d1=√r2−(102)2=√r2−25
For chord CD (length = 24 cm):
d2=√r2−(242)2=√r2−144
Step 4: Set Up the Equation
From the earlier step, we have:
d1+d2=17
Substituting the expressions for d1 and d2:
√r2−25+√r2−144=17
Step 5: Solve the Equation
To solve for r, we will isolate one of the square roots:
1. Rearranging gives:
√r2−144=17−√r2−25
2. Squaring both sides:
r2−144=(17−√r2−25)2
r2−144=289−34√r2−25+(r2−25)
r2−144=r2+264−34√r2−25
3. Simplifying:
−144−264=−34√r2−25
−408=−34√r2−25
√r2−25=40834=12
4. Squaring both sides again:
r2−25=144
r2=169
r=√169=13 cm
Conclusion
The radius of the circle is 13 cm.
---
We have two chords AB and CD in a circle. The lengths of the chords are given as:
- Length of AB = 10 cm
- Length of CD = 24 cm
Let O be the center of the circle. The perpendicular distance from the center O to the chord AB is denoted as d1, and the perpendicular distance from O to the chord CD is denoted as d2.
d1+d2=17 cm
The distance from the center of the circle to a chord can be found using the formula:
d=√r2−(l2)2
where r is the radius of the circle and l is the length of the chord.
d1=√r2−(102)2=√r2−25
d2=√r2−(242)2=√r2−144
From the earlier step, we have:
d1+d2=17
Substituting the expressions for d1 and d2:
√r2−25+√r2−144=17
To solve for r, we will isolate one of the square roots:
1. Rearranging gives:
√r2−144=17−√r2−25
r2−144=(17−√r2−25)2
r2−144=289−34√r2−25+(r2−25)
r2−144=r2+264−34√r2−25
−144−264=−34√r2−25
−408=−34√r2−25
√r2−25=40834=12
r2−25=144
r2=169
r=√169=13 cm
The radius of the circle is 13 cm.
Topper's Solved these Questions
Similar Questions
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords are on the same side of the centre and the distance between them is 3cm, then the diameter of the circle is.
View SolutionAB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
View Solution
Knowledge Check
AB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
A12 cmB13 cmC14 cmD16 cmIn a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. If both the chords are on the same side of the centre, then the distance between the chords is a
A9 cmB7 cmC23 cmD11 cmIn a circle, there are two chords opposite to the centre of the circle. The length of one chord and the radius of the circle is 6 cm and 5 cm respectively, and the distance between both the chords is 7 cm. Find the length of the second chord.
Aa) 8 cmBb) 10 cmCc) 6 cmDd) 14 cm
AB and CD are two parallel chords of a circle such that AB=10 cm and CD=24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo parallel chords AB and CD of lengths 6 and 12 cm, respectively, are 3 cm apart. Find the radius of the circle.
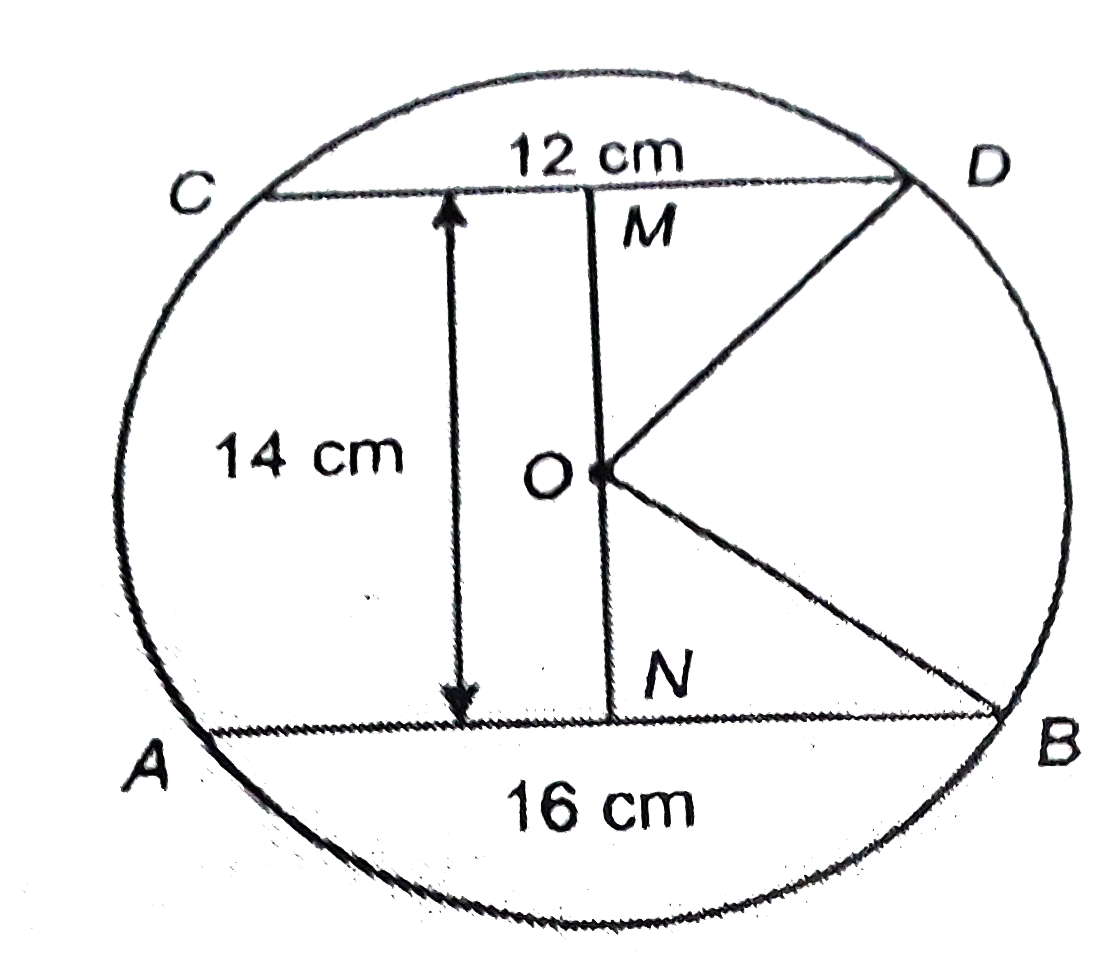
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View SolutionIn a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are
(i) on the same side of the centre.
(ii) on the opposite sides of the centre.
View Solution
