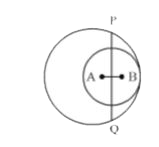
Two circles whose centres are A & B touches internally to each other as shown in figure their radii are 5 and 3 units respectively. The perpendicular bisector of AB meets at P and Q on the outer circle. Find the length of PQ.
4√6
4
2√6
2
The correct Answer is:4√6 cm
Step by step video, text & image solution for Two circles whose centres are A & B touches internally to each other as shown in figure their radii are 5 and 3 units respectively. The perpendicular bisector of AB meets at P and Q on the outer circle. Find the length of PQ. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the adjoining figure, two circle with centres at A and B, and of radii 5 cm and 3 cm touch each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.
View SolutionIn the figure, two circles with centres AandB and of radii 5cmand3cm touch each other intermally. If the perpendicular bisectors of segment AB meets the bigger circle in PandQ. Find the length of PQ.
View Solution
Knowledge Check
Two circles whose centres are A & B touches internally to each other as shown in figure their radii are 5 and 3 units respectively. The perpendicular bisector of AB meets at P and Q on the outer circle. Find the length of PQ.
 A4√6B4C2√6D2
A4√6B4C2√6D2Two circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cmB12 cmC9 cmD8 cmTwo circles of radii 13 cm and 5 cm touch internally each other. Find the distance between their centres:
A18 cmB12 cmC9 cmD8 cm
In Figure, two circles with centres A and B and of radii 5 cm and 3 cm touch each other internally. If the perpendicular bisector of segment AB meets the bigger circle in P and Q , find the length of PQ
Aand B are the centres of the circles with radii 5cm and 3cm respectively.
C is the mid-point of AB.
Extend AB upto O point on circumference of outer circle.
AB=AO−BO=5−3=2cm (since AO and BO are radii of larger and smaller circles)
AC=AB2=22=1cm
now in right angled triangle AMP,AC=1cm,AP=5cm
by pythagoras therom , AP2=PC2+AC2
PC2=√AP2−AC2
PC2=√52−12
Therefore,PQ=2PC=2√24
=4√6cm(CP=CQ)
View SolutionTwo circles are touches internally and their radii are 4 cm and 6 cm respectively. Find the largest chord drawn in the outer circle.
View SolutionA and B are centres of two circles whose radii are 5 cm and 2 cm respectively. The direct common tangent meets the extended AB point P. The P divides the AB-
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
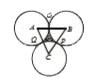
View SolutionThree circles with centres A, B and C and with unit radii touch each other at O, P and Q. Find the area of the shaded region .
View Solution
