Which of the following statements is/are correct?
The intersections of the angle bisectors of the quadrilateral are the vertices of the cyclic quadrilateral
If diagonals of a cyclic quadrilateral perpendicularly intersect at point P, then the line through P, perpendicular to any side bisects the opposite side.
The product of the lengths of the two diagonals of a cyclic quadrilateral is equal to the sum of the products of opposite sides.
(i) and (ii)
(ii) and (iii)
(i) and (iii)
all of these
The correct Answer is:C
To determine which of the statements regarding cyclic quadrilaterals are correct, we will analyze each statement step by step.
Step 1: Analyze the First Statement
Statement: The intersections of the angle bisectors of the quadrilateral are the vertices of the cyclic quadrilateral.
Analysis:
- A cyclic quadrilateral is defined as a quadrilateral whose vertices lie on the circumference of a circle.
- The angle bisectors of a quadrilateral do not necessarily intersect at points that can be the vertices of a cyclic quadrilateral.
- The intersection of the angle bisectors of a quadrilateral does not guarantee that these points will form a cyclic quadrilateral.
Conclusion: This statement is incorrect.
Step 2: Analyze the Second Statement
Statement: If diagonals of a cyclic quadrilateral perpendicularly intersect at point P, then the line through P, perpendicular to any side bisects the opposite side.
Analysis:
- In a cyclic quadrilateral, if the diagonals intersect at point P and are perpendicular, then any line drawn through P that is perpendicular to one side of the quadrilateral will indeed bisect the opposite side.
- This is based on the properties of cyclic quadrilaterals and perpendicular bisectors.
Conclusion: This statement is correct.
Step 3: Analyze the Third Statement
Statement: The product of the lengths of the two diagonals of a cyclic quadrilateral is equal to the sum of the products of opposite sides.
Analysis:
- This is a well-known theorem in geometry concerning cyclic quadrilaterals.
- Mathematically, if we denote the lengths of the diagonals as AC and BD, and the sides as AB, BC, CD, and DA, then the relationship can be expressed as:
AC⋅BD=AB⋅CD+AD⋅BC
- This relationship holds true for all cyclic quadrilaterals.
Conclusion: This statement is correct.
Final Conclusion
Based on the analysis:
- The first statement is incorrect.
- The second statement is correct.
- The third statement is correct.
Thus, the correct statements are the second and third statements.
---
Statement: The intersections of the angle bisectors of the quadrilateral are the vertices of the cyclic quadrilateral.
- A cyclic quadrilateral is defined as a quadrilateral whose vertices lie on the circumference of a circle.
- The angle bisectors of a quadrilateral do not necessarily intersect at points that can be the vertices of a cyclic quadrilateral.
- The intersection of the angle bisectors of a quadrilateral does not guarantee that these points will form a cyclic quadrilateral.
Statement: If diagonals of a cyclic quadrilateral perpendicularly intersect at point P, then the line through P, perpendicular to any side bisects the opposite side.
- In a cyclic quadrilateral, if the diagonals intersect at point P and are perpendicular, then any line drawn through P that is perpendicular to one side of the quadrilateral will indeed bisect the opposite side.
- This is based on the properties of cyclic quadrilaterals and perpendicular bisectors.
Statement: The product of the lengths of the two diagonals of a cyclic quadrilateral is equal to the sum of the products of opposite sides.
- This is a well-known theorem in geometry concerning cyclic quadrilaterals.
- Mathematically, if we denote the lengths of the diagonals as AC and BD, and the sides as AB, BC, CD, and DA, then the relationship can be expressed as:
AC⋅BD=AB⋅CD+AD⋅BC
- This relationship holds true for all cyclic quadrilaterals.
Based on the analysis:
- The first statement is incorrect.
- The second statement is correct.
- The third statement is correct.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ArectangleBsquareCparallelogramDcyclic quadrilateral
ArectangleBsquareCparallelogramDcyclic quadrilateralThe quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ArectangleBsquareCparallelogramDcyclic quadrilateral
ArectangleBsquareCparallelogramDcyclic quadrilateralIf the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is:
ArhombusBsquareCrectangleDnone of these
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionCyclic Quadrilateral and its properties
View SolutionABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
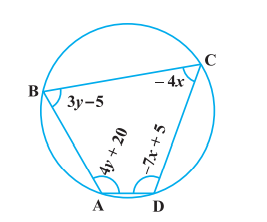
View SolutionIf the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a
View SolutionThe minimum value of the sum of the lengths of diagonals of a cyclic quadrilateral of area a2 square units, is
View Solution
