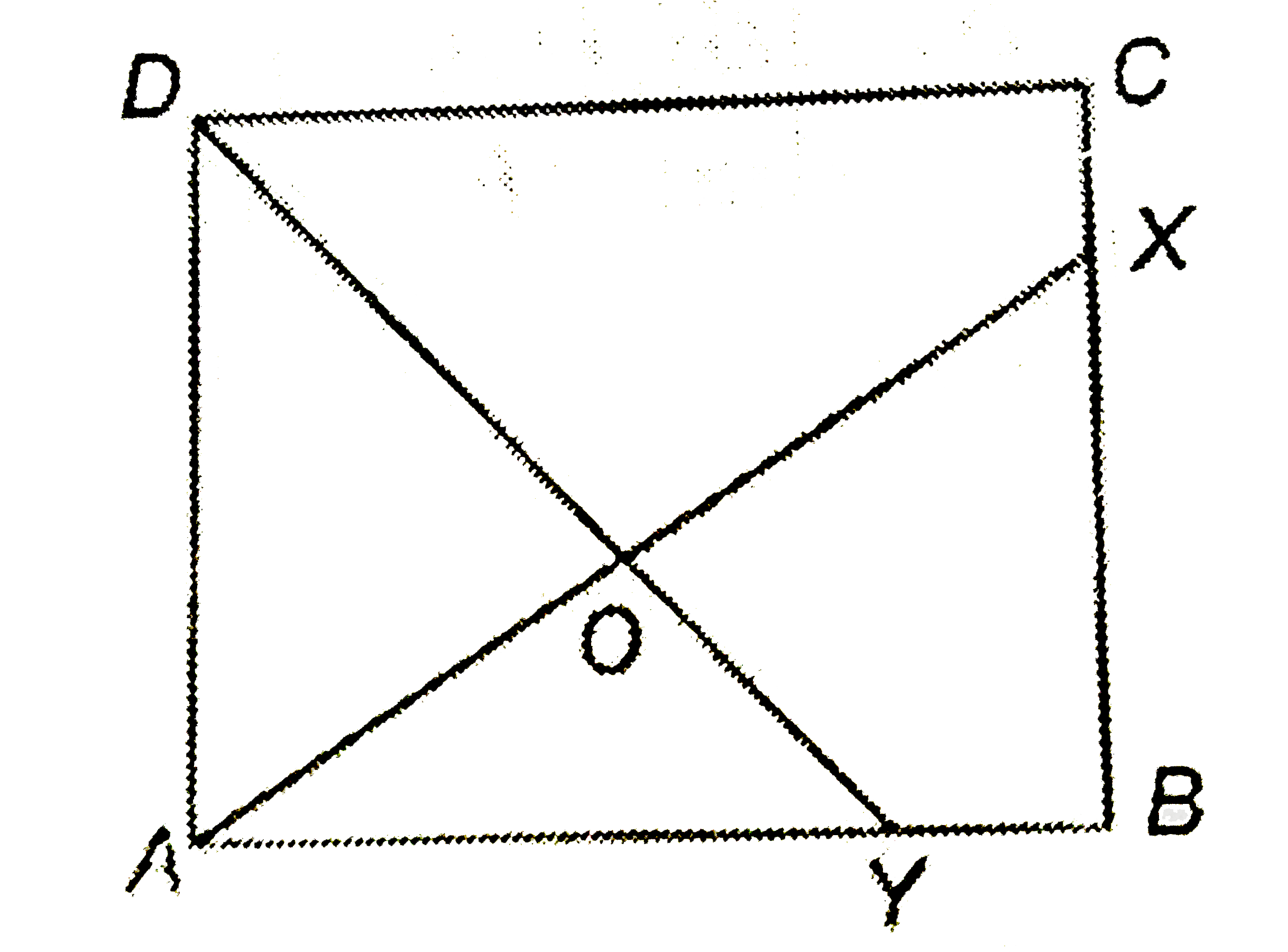
ABCD is a square, A is joined to a point P on BC and D is joined to a point Q on AB. If AP=DQ and AP intersects DQ at R the, ∠DRP is :
60∘
120∘
90∘
can't be determined
The correct Answer is:C
To solve the problem, we will follow these steps:
1. Draw the Square and Points:
- Draw square ABCD.
- Mark point P on side BC and point Q on side AB.
2. Identify Given Information:
- We know that AP=DQ and that lines AP and DQ intersect at point R.
3. Analyze Triangles:
- Consider triangles ADQ and BAP.
- Since ABCD is a square, we have AD=AB (both are sides of the square).
4. Use Congruence Criteria:
- In triangles ADQ and BAP:
- AD=AB (sides of the square).
- DQ=AP (given).
- ∠DAB=∠PAB=90∘ (angles in a square).
- By the RHS (Right angle-Hypotenuse-Side) criterion, triangles ADQ and BAP are congruent.
5. Conclude Angles:
- Since the triangles are congruent, we have:
- ∠DQA=∠PAB.
- Also, since ∠DAB=90∘, we can express:
- ∠BAD=∠DAP+∠PAB.
- Thus, ∠DAP+∠PAB=90∘.
6. Analyze Triangle ARD:
- In triangle ARD:
- The sum of angles in a triangle is 180∘.
- ∠ARD+∠ADR+∠DRA=180∘.
- We know ∠ADR+∠DRA=90∘ (from previous steps).
- Therefore, ∠ARD=180∘−90∘=90∘.
7. Conclusion:
- Since AP is perpendicular to DQ, we conclude that ∠DRP=90∘.
Final Answer: ∠DRP=90∘.
---
- Draw square ABCD.
- Mark point P on side BC and point Q on side AB.
- We know that AP=DQ and that lines AP and DQ intersect at point R.
- Consider triangles ADQ and BAP.
- Since ABCD is a square, we have AD=AB (both are sides of the square).
- In triangles ADQ and BAP:
- AD=AB (sides of the square).
- DQ=AP (given).
- ∠DAB=∠PAB=90∘ (angles in a square).
- By the RHS (Right angle-Hypotenuse-Side) criterion, triangles ADQ and BAP are congruent.
- Since the triangles are congruent, we have:
- ∠DQA=∠PAB.
- Also, since ∠DAB=90∘, we can express:
- ∠BAD=∠DAP+∠PAB.
- Thus, ∠DAP+∠PAB=90∘.
- In triangle ARD:
- The sum of angles in a triangle is 180∘.
- ∠ARD+∠ADR+∠DRA=180∘.
- We know ∠ADR+∠DRA=90∘ (from previous steps).
- Therefore, ∠ARD=180∘−90∘=90∘.
- Since AP is perpendicular to DQ, we conclude that ∠DRP=90∘.
Topper's Solved these Questions
Similar Questions
In a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY.
View SolutionLet ABCD be a square. An arc of a circle with A as centre and AB as radius is drawn inside the square joining the points B and D. Points P on AB, S on AD, Q and R on arc BD are taken such that PQRS is a square. Further suppose that PQ and RS are parallel toAC. Then, areaPQRSareaABCD is
View Solution
Knowledge Check
In a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY.
 A60∘B120∘C90∘Dcan't be determined
A60∘B120∘C90∘Dcan't be determinedABCD is a square. M is the mid-point of AB and N is the mid-point of BC. DM and AN are joined and they meet at O, then which of the following is correct ?
AOA : OM = 1 : 2BAN = MDC∠ADM=∠ANBD∠AMD=∠BANLet ABCD be a square. An arc of a circle with A as centre and AB as radius is drawn inside the square joining the points B and D. Points P on AB, S on AD,Q and R on are taken such that PQRS is a square. Further suppose that PQ and RS are parallel to AC. ThenareaPQRSareaABCD is
A18B15C14D25
In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).

View SolutionThe vertex A of the parabola y2=4ax is joined to any point P on it and PQ is drawn at right angles to AP to meet the axis in Q. Projection of PQ on the axis is equal to
View SolutionABCD is a parallelogram. E is a point on extended side AB such that AB = BE. By joining D to E it intersects side BC at P. Find length of PC if BC = 15 cm.
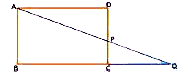
View SolutionIn the given figure,ABCD is a rectangle and P is a point on DC such that BC=24 cm, DP = 10 cm, and CD=15 cm .If AP produced intersect BC produced at Q. then find the length of AQ.
View SolutionD and E are the mid-points of the sides AB and AC of ΔABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
View Solution