PQRS is a parallelogram in which
and . How many points in the plane of the quadrilateral are there such that a point is equidistant from its vertices ?
0
1
2
3
The correct Answer is:A
To solve the problem, we need to analyze the properties of the given quadrilateral PQRS and determine if it can be classified as a parallelogram based on the angles provided.
1. Identify the Properties of a Parallelogram:
- In a parallelogram, opposite angles are equal.
- The sum of the angles in any quadrilateral is 360 degrees.
2. Given Angles:
- Angle P = 70 degrees
- Angle Q = 90 degrees
- Angle R = 100 degrees
- We need to find Angle S.
3. Calculate Angle S:
- Using the property that the sum of angles in a quadrilateral is 360 degrees:
Angle S=360∘−(Angle P+Angle Q+Angle R)
Angle S=360∘−(70∘+90∘+100∘)=360∘−260∘=100∘
4. Check Opposite Angles:
- Now we have:
- Angle P = 70 degrees
- Angle Q = 90 degrees
- Angle R = 100 degrees
- Angle S = 100 degrees
- We see that Angle R and Angle S are equal (100 degrees), but Angle P (70 degrees) is not equal to Angle Q (90 degrees).
5. Conclusion:
- Since the angles do not satisfy the properties of a parallelogram (specifically, opposite angles must be equal), PQRS cannot be classified as a parallelogram.
- Therefore, there are no points in the plane that are equidistant from the vertices of PQRS.
6. Final Answer:
- The number of points in the plane that are equidistant from the vertices of quadrilateral PQRS is 0.
- In a parallelogram, opposite angles are equal.
- The sum of the angles in any quadrilateral is 360 degrees.
- Angle P = 70 degrees
- Angle Q = 90 degrees
- Angle R = 100 degrees
- We need to find Angle S.
- Using the property that the sum of angles in a quadrilateral is 360 degrees:
Angle S=360∘−(Angle P+Angle Q+Angle R)
Angle S=360∘−(70∘+90∘+100∘)=360∘−260∘=100∘
- Now we have:
- Angle P = 70 degrees
- Angle Q = 90 degrees
- Angle R = 100 degrees
- Angle S = 100 degrees
- We see that Angle R and Angle S are equal (100 degrees), but Angle P (70 degrees) is not equal to Angle Q (90 degrees).
- Since the angles do not satisfy the properties of a parallelogram (specifically, opposite angles must be equal), PQRS cannot be classified as a parallelogram.
- Therefore, there are no points in the plane that are equidistant from the vertices of PQRS.
- The number of points in the plane that are equidistant from the vertices of quadrilateral PQRS is 0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC=70∘ , ∠BAC is 30∘ , find ∠ BCD. Further if AB=BC, find ∠ ECD.
AA. 80* and 50*BB. 30* and 80*CC. 100* and 70*DD. none of thesePQRS is a kite. ∠P=70∘,∠S=90.5∘,∠R equals
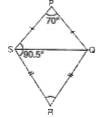 A99∘B91∘C111∘D109∘
A99∘B91∘C111∘D109∘PQRs is a cyclic quadrilateral. Find the measure of ∠Pand∠Q.
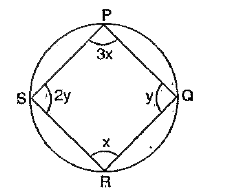 A135∘,60∘B60∘,120∘C60∘,90∘D100∘,120∘
A135∘,60∘B60∘,120∘C60∘,90∘D100∘,120∘
In a parallelogram PQRS, the bisectors of ∠P and ∠Q meet at O. Find ∠POQ.
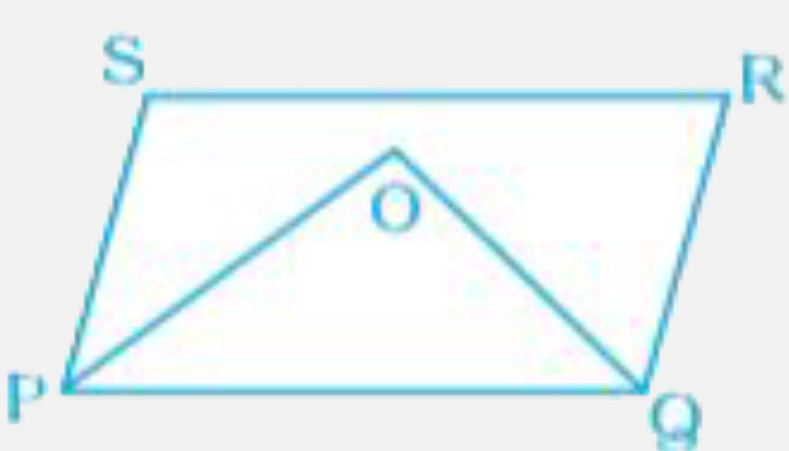
View Solution□PQRS is a parallelogram . The ratio measure of ∠Pand∠R is 3:7 . Find the measure of ∠P.
View SolutionIn a △PQR,∠P=110∘, PQ = PR . Find ∠Qand∠R
View SolutionIn ΔPQR,∠P=50∘and∠Q=60∘. Find ∠R
View SolutionIn a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
View Solution
