Question

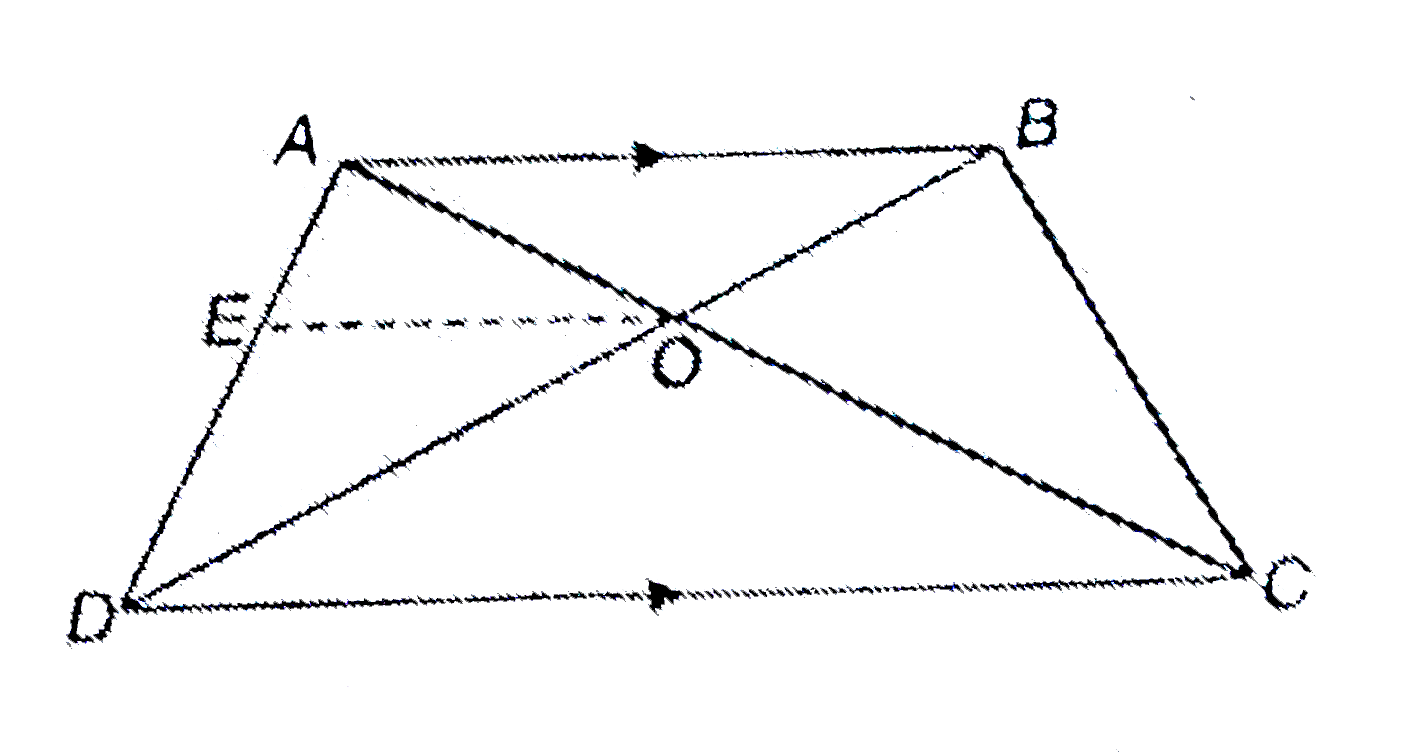
In a trapezium ABCD, where AB||CD and diagonal AC intersects the other diagonal BD at O. If a line segment EF parallel to AB and CD passes through the point O, where E lies on AD and F lies on BC, find the length of EF, provided AB=6 cm and CD = 2 cm.

Options

A. A)3 cm
B. B)4 cm
C. C)4.5 cm
D. D)none of these

Answer

A

Explanation

To find the length of the line segment EF that is parallel to AB and CD in trapezium ABCD, we can use the properties of similar triangles. Here is the step-by-step solution:

Step 1: Identify the trapezium and its properties
We have trapezium ABCD where AB is parallel to CD. Given that AB = 6 cm and CD = 2 cm, we can denote:
- Length of AB (top base) = 6 cm
- Length of CD (bottom base) = 2 cm

Step 2: Draw the diagonals
Draw diagonals AC and BD which intersect at point O. This creates two triangles: ΔAOB and ΔCOD.

Step 3: Establish similarity of triangles
Since AB || CD, triangles AOB and COD are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This means that the ratios of their corresponding sides are equal.

Step 4: Set up the ratio of the bases
Let the height from point O to line AB be h1 and the height from point O to line CD be h2. The ratio of the bases AB and CD gives us:
\( \frac{AB}{CD} = \frac{h1}{h2} \)
Substituting the values:
\( \frac{6}{2} = \frac{h1}{h2} \)
This simplifies to:
\( \frac{h1}{h2} = 3 \)
This means that for every 3 units of height from O to AB, there is 1 unit of height from O to CD.

Step 5: Determine the ratio of heights
Let’s denote the height from O to CD as h2 = 1k and from O to AB as h1 = 3k, where k is a common factor.

Step 6: Find the length of EF using the section formula
Since EF is parallel to both AB and CD, we can use the section formula to find its length. The length of EF can be calculated as:
\( EF = CD + \frac{(AB - CD) \cdot h2}{h1 + h2} \)
Substituting the known values:
\( EF = 2 + \frac{(6 - 2) \cdot 1}{3 + 1} \)
\( EF = 2 + \frac{4 \cdot 1}{4} \)
\( EF = 2 + 1 \)
\( EF = 3 \, \text{cm} \)

Final Answer
The length of segment EF is 3 cm.

---