Let ABCD be a square. An arc of a circle with A as centre and AB as radius is drawn inside the square joining the points B and D. Points P on AB, S on AD, Q and R on arc BD are taken such that PQRS is a square. Further suppose that PQ and RS are parallel toAC. Then, areaPQRSareaABCD is
18
15
14
25
To solve the problem, we need to find the ratio of the area of square PQRS to the area of square ABCD. Let's break this down step by step.
Step 1: Understand the Geometry
Let’s denote the side length of square ABCD as a. The area of square ABCD is given by:
Area of ABCD=a2
Step 2: Identify Points and Coordinates
Place the square ABCD in the coordinate system:
- Point A at (0, 0)
- Point B at (a, 0)
- Point C at (a, a)
- Point D at (0, a)
The center of the arc is at point A (0, 0), and the radius is the length of side AB, which is a.
Step 3: Define the Square PQRS
Let the side length of square PQRS be k. Since PQ and RS are parallel to AC, we can place points P and S on sides AB and AD, respectively:
- Let point P be at (x1, 0) on AB
- Let point S be at (0, y1) on AD
Step 4: Coordinates of Points Q and R
Since PQRS is a square, the coordinates of points Q and R can be derived as follows:
- Point Q will be at (x1 + k, k) (moving k units up from P)
- Point R will be at (k, y1 + k) (moving k units right from S)
Step 5: Equation of the Arc
The arc BD is part of the circle centered at A with radius a. The equation of the circle is:
x2+y2=a2
Since points Q and R lie on this arc, we can substitute their coordinates into the circle’s equation.
Step 6: Set Up the Equations
For point Q:
(x1+k)2+k2=a2
For point R:
k2+(y1+k)2=a2
Step 7: Express y1 in terms of x1
Since PQRS is a square, the relationship between y1 and x1 can be established. From the square’s properties:
y1=x1
Step 8: Substitute and Solve
Substituting y1=x1 into the equations derived from the arc:
1. For Q:
(x1+k)2+k2=a2
Expanding gives:
x12+2kx1+k2+k2=a2⟹x12+2kx1+2k2=a2
2. For R:
k2+(x1+k)2=a2
This will yield a similar equation.
Step 9: Solve for k
By solving these equations simultaneously, we can express k2 in terms of a2.
Step 10: Calculate the Area of PQRS
The area of square PQRS is:
Area of PQRS=k2
Step 11: Find the Ratio
The ratio of the area of square PQRS to the area of square ABCD is:
Area of PQRSArea of ABCD=k2a2
Conclusion
After solving the equations, we find that this ratio simplifies to:
12
Let’s denote the side length of square ABCD as a. The area of square ABCD is given by:
Area of ABCD=a2
Place the square ABCD in the coordinate system:
- Point A at (0, 0)
- Point B at (a, 0)
- Point C at (a, a)
- Point D at (0, a)
Let the side length of square PQRS be k. Since PQ and RS are parallel to AC, we can place points P and S on sides AB and AD, respectively:
- Let point P be at (x1, 0) on AB
- Let point S be at (0, y1) on AD
Since PQRS is a square, the coordinates of points Q and R can be derived as follows:
- Point Q will be at (x1 + k, k) (moving k units up from P)
- Point R will be at (k, y1 + k) (moving k units right from S)
The arc BD is part of the circle centered at A with radius a. The equation of the circle is:
x2+y2=a2
Since points Q and R lie on this arc, we can substitute their coordinates into the circle’s equation.
For point Q:
(x1+k)2+k2=a2
For point R:
k2+(y1+k)2=a2
Since PQRS is a square, the relationship between y1 and x1 can be established. From the square’s properties:
y1=x1
Substituting y1=x1 into the equations derived from the arc:
1. For Q:
(x1+k)2+k2=a2
Expanding gives:
x12+2kx1+k2+k2=a2⟹x12+2kx1+2k2=a2
k2+(x1+k)2=a2
This will yield a similar equation.
By solving these equations simultaneously, we can express k2 in terms of a2.
The area of square PQRS is:
Area of PQRS=k2
The ratio of the area of square PQRS to the area of square ABCD is:
Area of PQRSArea of ABCD=k2a2
After solving the equations, we find that this ratio simplifies to:
12
Similar Questions
Side of square ABCD is 7 cm with D as the centre and DA as radius, arc XC is drawn. Find the area of the shaded region with the help of the following flow chart.

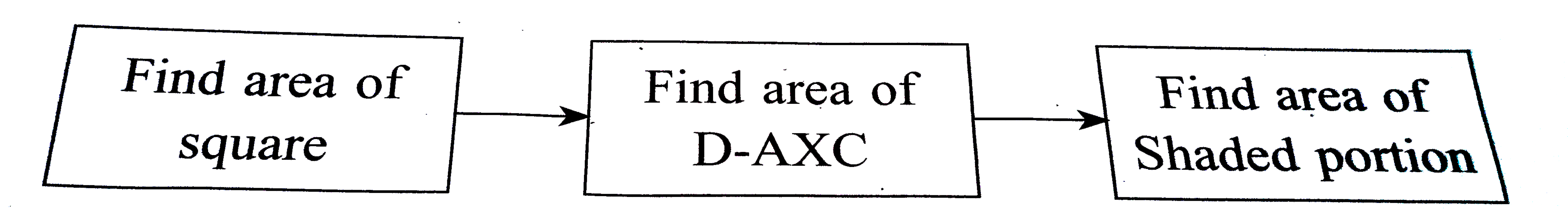
View SolutionIn the figure, side of square ABCD is 7 cm. With centre D and radius DA, sector D-AXC is drawn. Find the area of the shaded region.

View Solution
Knowledge Check
Let ABCD be a square. An arc of a circle with A as centre and AB as radius is drawn inside the square joining the points B and D. Points P on AB, S on AD,Q and R on are taken such that PQRS is a square. Further suppose that PQ and RS are parallel to AC. ThenareaPQRSareaABCD is
A18B15C14D25Plot the points P(1, 0), Q(4,0) and S(1, 3). Find the coordinates of the point R such that PQRS is a square.
A(2,3)B(3,3)C(4,3)D(0,3)ABCD is a square, A is joined to a point P on BC and D is joined to a point Q on AB. If AP=DQ and AP intersects DQ at R the, ∠DRP is :
A60∘B120∘C90∘Dcan't be determined
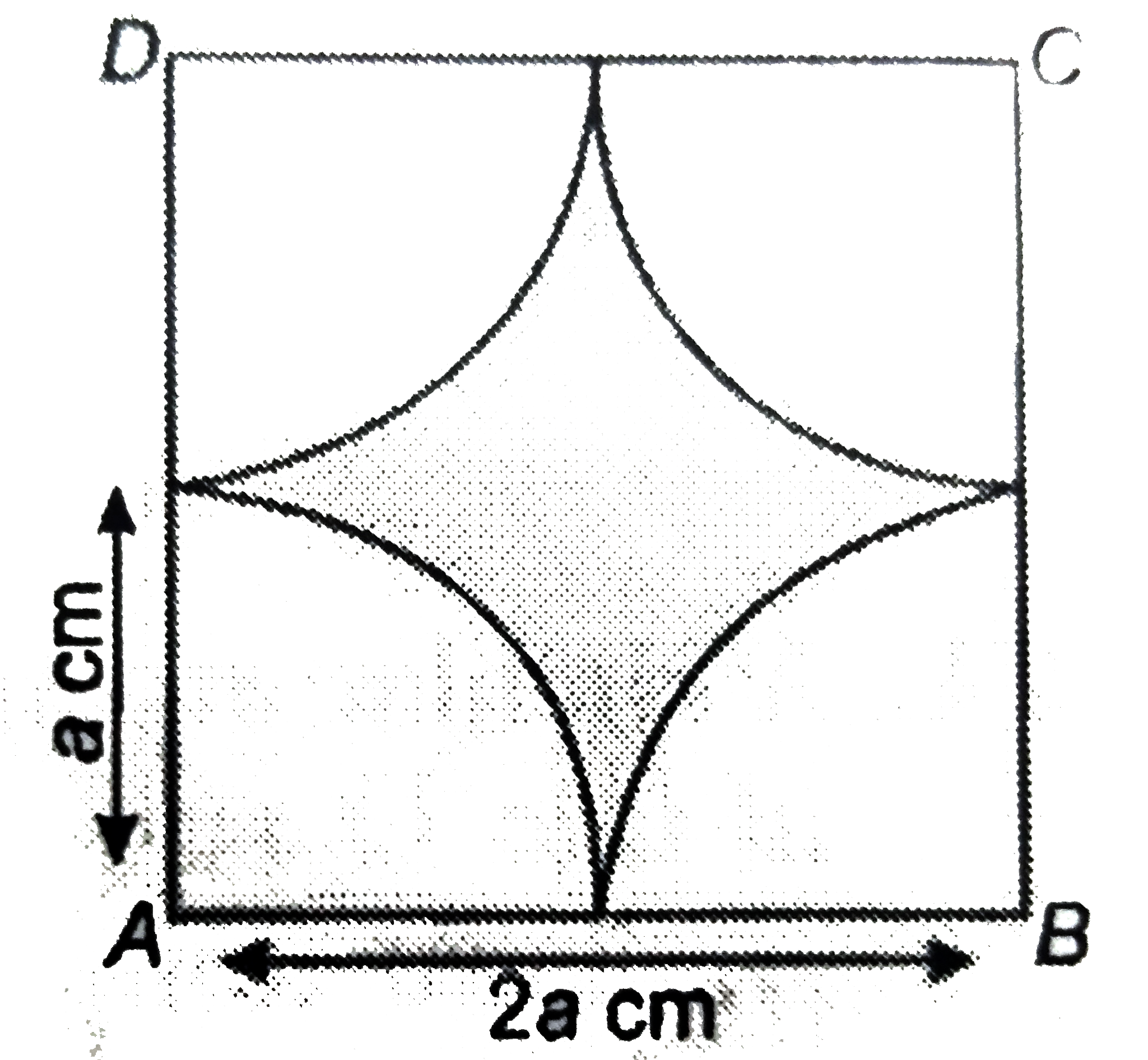
In the square ABCD with side 2acm, four quarter circles are drawn with the vertices as centres and radius acm. Find the area of the shaded portion.
View SolutionADandBC are the arcs of concentric circles with O as their common centre. If OA=AB. then the area of the figure ABCD is
View SolutionIn the given figure, side of square ABCD is 7 cm. With centre D and radius DA, sector D-AXC is drawn. find out the area of the shaded ragion.
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionIn a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY.
View Solution