Using dimensions method show that the speed of sound in a material medium of modulus of elasticity E and density ρ is v∝√Eρ
To show that the speed of sound v in a material medium with modulus of elasticity E and density ρ is proportional to √Eρ using the dimensions method, we can follow these steps:
Step 1: Define the relationship
Assume that the speed of sound v is proportional to the modulus of elasticity E and density ρ:
v∝Exρy
where x and y are the powers to which E and ρ are raised, respectively.
Step 2: Write the dimensions
Next, we need to write the dimensions of each quantity involved:
- The dimension of speed v is:
(v)=(L)(T−1)=L1T−1
- The modulus of elasticity E is defined as stress over strain. The dimension of stress is force per unit area:
(E)=(F)(A)=(M)(L)(T−2)(L2)=ML−1T−2
- The density ρ is mass per unit volume:
(ρ)=(M)(L3)=ML−3
Step 3: Substitute dimensions into the equation
Substituting the dimensions into the equation v∝Exρy:
(L1T−1)=(ML−1T−2)x(ML−3)y
This expands to:
L1T−1=MxL−xT−2x⋅MyL−3y
Combining the dimensions gives:
L1T−1=Mx+yL−x−3yT−2x
Step 4: Equate dimensions
Now we equate the dimensions on both sides:
1. For mass M:
x+y=0(1)
2. For length L:
−x−3y=1(2)
3. For time T:
−2x=−1(3)
Step 5: Solve the equations
From equation (3):
2x=1⟹x=12
Substituting x=12 into equation (1):
12+y=0⟹y=−12
Now substituting x and y into equation (2) to verify:
−12−3(−12)=−12+32=1(True)
Step 6: Write the final relationship
Thus, we have:
v∝E12ρ−12
This can be rewritten as:
v∝√Eρ
Conclusion
Therefore, we have shown that the speed of sound v in a material medium is proportional to √Eρ.
---
Assume that the speed of sound v is proportional to the modulus of elasticity E and density ρ:
v∝Exρy
where x and y are the powers to which E and ρ are raised, respectively.
Next, we need to write the dimensions of each quantity involved:
- The dimension of speed v is:
(v)=(L)(T−1)=L1T−1
- The modulus of elasticity E is defined as stress over strain. The dimension of stress is force per unit area:
(E)=(F)(A)=(M)(L)(T−2)(L2)=ML−1T−2
- The density ρ is mass per unit volume:
(ρ)=(M)(L3)=ML−3
Substituting the dimensions into the equation v∝Exρy:
(L1T−1)=(ML−1T−2)x(ML−3)y
This expands to:
L1T−1=MxL−xT−2x⋅MyL−3y
Combining the dimensions gives:
L1T−1=Mx+yL−x−3yT−2x
Now we equate the dimensions on both sides:
1. For mass M:
x+y=0(1)
2. For length L:
−x−3y=1(2)
3. For time T:
−2x=−1(3)
From equation (3):
2x=1⟹x=12
Substituting x=12 into equation (1):
12+y=0⟹y=−12
Now substituting x and y into equation (2) to verify:
−12−3(−12)=−12+32=1(True)
Thus, we have:
v∝E12ρ−12
This can be rewritten as:
v∝√Eρ
Therefore, we have shown that the speed of sound v in a material medium is proportional to √Eρ.
Topper's Solved these Questions
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
10 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - LONG ANSWER QUESTIONS
3 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
Similar Questions
If v stands for velocity of sound, E is elasticity and d the density, then find x in the equation v=(dE)x
View SolutionThe time period of oscillation T of a small drop of liquid under surface tension depends upon the density ρ, the radius r and surface tension σ. Using dimensional analysis show that T∝√ρr3σ
View Solution(A) : Relative to an observer at rest in a medium the speed of a mechanical wave in that medium (1) depends only on elastic and other properties (such as mass density) of the medium. It does not depend on the velocity of the source.
(B): For an observer moving with velocity v0 relative to the medium, the speed of a wave is obviously different from v and is given by v±v0
View SolutionA metallic wire of length l is held between two rigid supports. If the wire is cooled through a temperature t. (Y= Young's modulus of elasticity of wire, ρ= density, α= thermal coefficient of linear expansion). Then the frequency of oscillation is proportional to
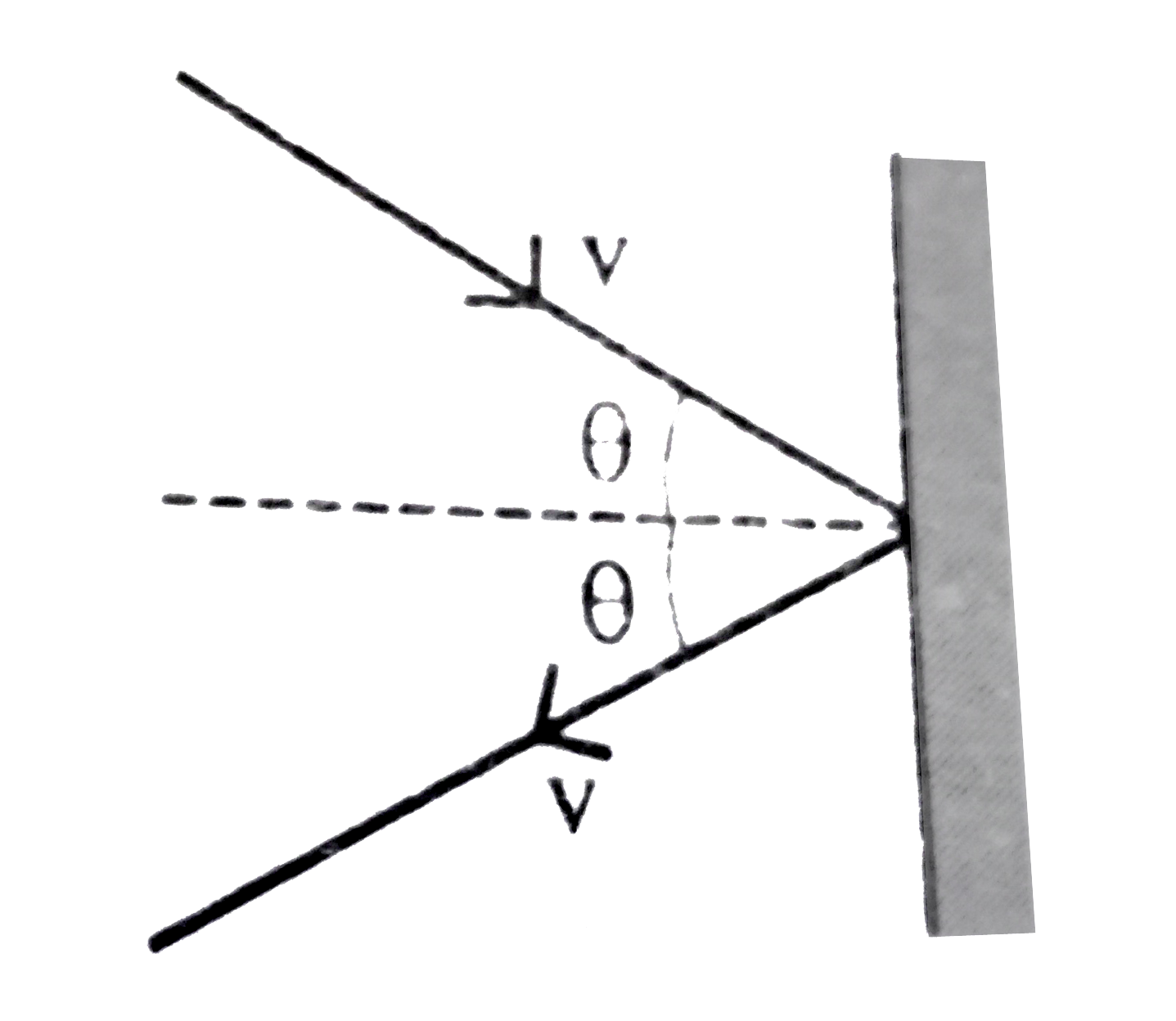
View SolutionA jet water, whose cross section is A strikes a wall making an angle θ with normal and elastically rebounds. The velocity of water of density ρ is v. Force exerted on wall is :-
View SolutionA block of material has a density ρ1 and floats three-fourth submerged in a liquid of unknown density. Show tht the density ρ2 of the unknown liquid is given by ρ2=43ρ1.
View Solutionv1andv2 are the velocities of sound at the same temperature in two monoatomic gases of densities ρ1andρ2 respectively. If ρ1ρ2=14 then the ratio of velocities v1andv2 is
View SolutionObtain the dimensions of linear momentum and surface tension in terms of velocity (v), density (ρ) and frequency(ν) as fundamental units.
View SolutionTwo block each of mass 'm' are attached with two elastic strings as shown in the figure. Masses of strings are negligible in comparison to block of mass 'm' density of material of each string is ρ. The whole system is moving vertically upward with an acceleration a = g/2. It is in equilibrium with respect to elevator.
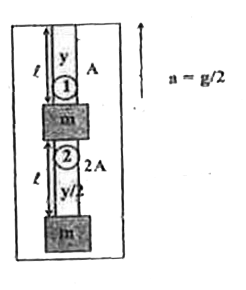
Ratio of elongation in rod 1 to that of rod 2 will be
View SolutionA spherical solild of volume V is made of a material of density ρ1. It is falling through a liquid of density ρ2(ρ2<ρ1). Assume that the liquid applies a viscous froce on the ball that is proportional ti the its speed v, i.e., Fviscous=−kv2(k>0). The terminal speed of the ball is
View Solution
