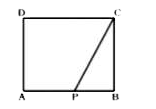
ABCD is a rectangle. There are two points P & Q on side AB and AD such that area of triangles PAQ, CDQ & PBC are equal. If the length of BP is 2 cm, find the length of AP.
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Define the Variables
Let:
- AP=x (the length we need to find)
- BP=2 cm (given)
- AQ=y (length of segment from A to Q)
- DQ=z (length of segment from D to Q)
Since AB is a rectangle, we know that:
- AB=AP+BP=x+2
- CD=AB=x+2 (opposite sides of a rectangle are equal)
- BC=AQ+DQ=y+z
Step 2: Area of the Triangles
The areas of the triangles are given to be equal:
1. Area of triangle PAQ:
AreaPAQ=12×AP×AQ=12×x×y
2. Area of triangle CDQ:
AreaCDQ=12×DQ×CD=12×z×(x+2)
3. Area of triangle PBC:
AreaPBC=12×BC×PB=12×(y+z)×2=(y+z)
Step 3: Set Up the Equations
Since the areas are equal, we can set up the following equations:
1. From AreaPAQ=AreaCDQ:
12xy=12z(x+2)⟹xy=z(x+2)(1)
2. From AreaCDQ=AreaPBC:
12z(x+2)=(y+z)(2)
Step 4: Solve the Equations
From equation (1):
z=xyx+2
Substituting z into equation (2):
xyx+2(x+2)=y+xyx+2
This simplifies to:
xy=y+xyx+2
Multiplying through by (x+2):
xy(x+2)=y(x+2)+xy
This simplifies to:
xyx+2xy=yx+2y+xy
Rearranging gives:
xyx+2xy−yx−xy−2y=0
This simplifies to:
xyx+xy−yx−2y=0
Factoring out y:
y(x−2)+xy=0
Thus, we can express z in terms of y:
z=2yx
Step 5: Substitute Back
Substituting z back into equation (1):
xy=2yx(x+2)
This simplifies to:
x2y=2y+4y⟹x2y=6y
Assuming y≠0:
x2=6⟹x=√6
Conclusion
Thus, the length of AP is √6 cm.
Let:
- AP=x (the length we need to find)
- BP=2 cm (given)
- AQ=y (length of segment from A to Q)
- DQ=z (length of segment from D to Q)
- AB=AP+BP=x+2
- CD=AB=x+2 (opposite sides of a rectangle are equal)
- BC=AQ+DQ=y+z
The areas of the triangles are given to be equal:
1. Area of triangle PAQ:
AreaPAQ=12×AP×AQ=12×x×y
2. Area of triangle CDQ:
AreaCDQ=12×DQ×CD=12×z×(x+2)
3. Area of triangle PBC:
AreaPBC=12×BC×PB=12×(y+z)×2=(y+z)
Since the areas are equal, we can set up the following equations:
1. From AreaPAQ=AreaCDQ:
12xy=12z(x+2)⟹xy=z(x+2)(1)
2. From AreaCDQ=AreaPBC:
12z(x+2)=(y+z)(2)
From equation (1):
z=xyx+2
xyx+2(x+2)=y+xyx+2
This simplifies to:
xy=y+xyx+2
Multiplying through by (x+2):
xy(x+2)=y(x+2)+xy
This simplifies to:
xyx+2xy=yx+2y+xy
Rearranging gives:
xyx+2xy−yx−xy−2y=0
This simplifies to:
xyx+xy−yx−2y=0
Factoring out y:
y(x−2)+xy=0
Thus, we can express z in terms of y:
z=2yx
Substituting z back into equation (1):
xy=2yx(x+2)
This simplifies to:
x2y=2y+4y⟹x2y=6y
Assuming y≠0:
x2=6⟹x=√6
Thus, the length of AP is √6 cm.
Topper's Solved these Questions
- QUADRILATERALBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:QUADRILATERALExercise:EXERCISE
Explore 48 Videos
- PROFIT & LOSSBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:PROFIT & LOSSExercise:Questions
Explore 200 Videos
- RATIO & PROPORTIONBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:RATIO & PROPORTIONExercise:QUESTIONS
Explore 113 Videos
Similar Questions
Knowledge Check
In ΔABC the straight line parallel to the side BCmeets ABandACat the points PandQ respectively. If AP=QC, the length of ABis 12 units and the length of AQis 2 units, then the length (in units) of CQ is
A4B6C8D10ABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
A10 cmB5 cmC20 cmD12 cmIn a ΔABC, D and E are two points on AB and AC respectively, and DE ∥ BC. If the length of AD and AB is 5 cm and 10 cm respectively, then find the ratio between the area of ΔABC and area of Quadrilateral DECB.
A4:1B3:5C4:3D5:2
ABCD is a rectangle. P is a point on the side AB as shown in the given figure . If DP = 13 CP = 10 and BP = 6 , then what is the value of AP ?
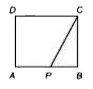
View SolutionABCD is a rectangle. P & Q are two points on AB, such that AP : PQ : QB = 3 : 4 : 5. Find the ratio of area ΔPQC and rectangle ABCD.
View SolutionIn a rectangle ABCD, diagonal AC and BD intersect each other at 0.If AB=32 cm and AD = 24 cm, find the length of OD.
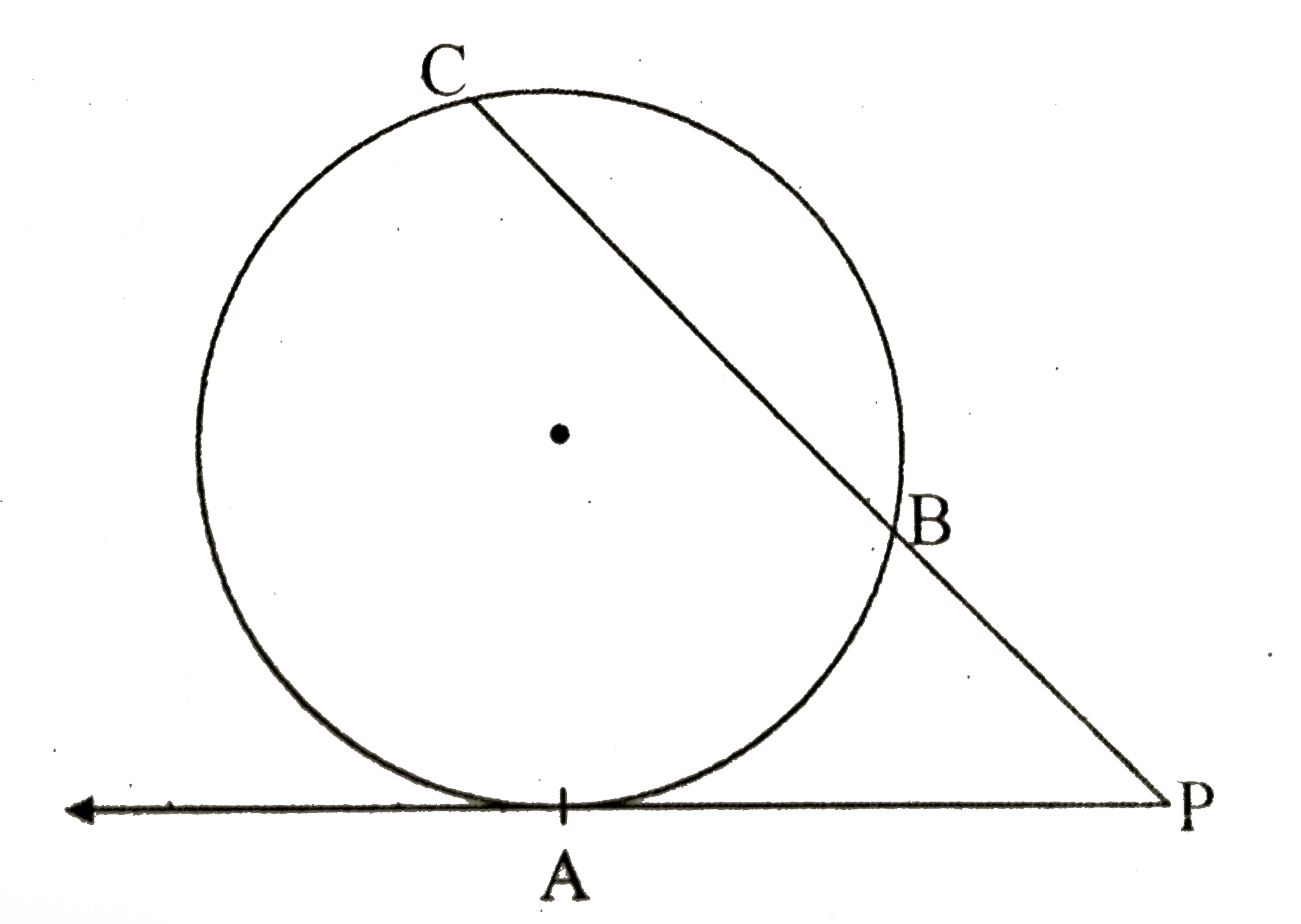
View SolutionIn the given figure, a tangent segment PA touching a circle in A and a secant PBC are shown. If AP = 15 cm and BP = 10 cm, find the length of PC.
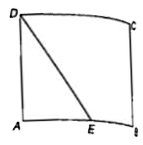
View SolutionABCD is a square , E is a point on AB such that BE=17 cm. The area of triangle ADE is 84 cm2 . What is the area of square ?
View Solution