A circle is inscribed in Δ PQR having sides 8 cm, 10 cm and 12 cm. A circle touches the sides PQ, QR and RP at D, E and F. Find PD
5 cm
6 cm
4 cm
10 cm
The correct Answer is:A
To find the length of PD in triangle PQR, where a circle is inscribed, we can follow these steps:
Step 1: Identify the sides of the triangle
The sides of triangle PQR are given as:
- PQ = 8 cm
- QR = 10 cm
- PR = 12 cm
Step 2: Understand the properties of tangents
When a circle is inscribed in a triangle, the points where the circle touches the sides are called the points of tangency. The lengths of the tangents drawn from an external point to a circle are equal.
Step 3: Assign variables to the tangent segments
Let:
- PD = x (the length we want to find)
- DQ = 8 - x (since PQ = PD + DQ = 8 cm)
- QE = y (the tangent from Q to the circle)
- ER = 10 - y (since QR = QE + ER = 10 cm)
- RF = z (the tangent from R to the circle)
- FP = 12 - z (since PR = RF + FP = 12 cm)
Step 4: Set up equations based on the tangent properties
From the properties of tangents:
1. PD = PF (since they are tangents from point P)
- Therefore, PD = PF = x
2. DQ = QE (since they are tangents from point Q)
- Therefore, DQ = QE = 8 - x
3. ER = RF (since they are tangents from point R)
- Therefore, ER = RF = 10 - y
Step 5: Relate the segments to the sides of the triangle
From the triangle's side lengths, we can write:
- For side PQ: PD + DQ = 8
- Thus, x + (8 - x) = 8
- For side QR: QE + ER = 10
- Thus, (8 - x) + (10 - y) = 10
- For side PR: PF + FP = 12
- Thus, x + (12 - z) = 12
Step 6: Solve for x
From the equation for side PR:
- x + (12 - z) = 12
- This simplifies to z = 12 - x
From the equation for side QR:
- (8 - x) + (10 - (12 - x)) = 10
- Simplifying gives: 8 - x + 10 - 12 + x = 10
- Which simplifies to: 6 = 10 (not useful)
Instead, we can directly use the relationship:
- Since PD = PF, we can say:
- PD + PF = PR
- x + x = 12
- 2x = 12
- x = 6
Step 7: Find PD
Thus, PD = x = 6 cm.
Final Answer
PD = 6 cm.
---
The sides of triangle PQR are given as:
- PQ = 8 cm
- QR = 10 cm
- PR = 12 cm
When a circle is inscribed in a triangle, the points where the circle touches the sides are called the points of tangency. The lengths of the tangents drawn from an external point to a circle are equal.
Let:
- PD = x (the length we want to find)
- DQ = 8 - x (since PQ = PD + DQ = 8 cm)
- QE = y (the tangent from Q to the circle)
- ER = 10 - y (since QR = QE + ER = 10 cm)
- RF = z (the tangent from R to the circle)
- FP = 12 - z (since PR = RF + FP = 12 cm)
From the properties of tangents:
1. PD = PF (since they are tangents from point P)
- Therefore, PD = PF = x
2. DQ = QE (since they are tangents from point Q)
- Therefore, DQ = QE = 8 - x
3. ER = RF (since they are tangents from point R)
- Therefore, ER = RF = 10 - y
From the triangle's side lengths, we can write:
- For side PQ: PD + DQ = 8
- Thus, x + (8 - x) = 8
- For side QR: QE + ER = 10
- Thus, (8 - x) + (10 - y) = 10
- For side PR: PF + FP = 12
- Thus, x + (12 - z) = 12
From the equation for side PR:
- x + (12 - z) = 12
- This simplifies to z = 12 - x
- (8 - x) + (10 - (12 - x)) = 10
- Simplifying gives: 8 - x + 10 - 12 + x = 10
- Which simplifies to: 6 = 10 (not useful)
- Since PD = PF, we can say:
- PD + PF = PR
- x + x = 12
- 2x = 12
- x = 6
Thus, PD = x = 6 cm.
PD = 6 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A circle is inscribed in Δ PQR having sides 8 cm, 10 cm and 12 cm. A circle touches the sides PQ, QR and RP at D, E and F. Find PD
A5 cmB6 cmC4 cmD10 cmThe area of circle inscribed in an equilateral triangle of side 12 cm is
A12cm2Bπcm2C12πcm2DNone of these
A circle is inscribed in △ABC having sides AB=8cm, BC=7cm and AC=5cm. Find AD, BE and CF.
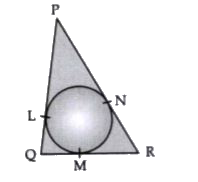
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionVarun has been selected by his School to design logo for Sports Day T-shirts for students and staff . The logo design is as given in the figure and he is working on the

fonts and different colours according to the theme. In given figure, a circle with centre O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively.

if radius of the circle is 4 cm , Find the area of ΔAOB.
View SolutionIn fig , a circle isinscribed in a triangle PQR with PQ = 10 cm , QR = 8 cm and PR = 12 cm .Find the length of the QM , RN and PL.
View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. The equation of circle C is
View SolutionThe sides of a triangle are 8 cm, 10 cm and 12 cm, find the greatest angle.
View Solution